Refine listing
Actions for selected content:
285 results in 20Mxx
THE ÉTALE GROUPOID OF AN INVERSE SEMIGROUP AS A GROUPOID OF FILTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 15 May 2013, pp. 234-256
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
ON THE
 $\ast $-SEMISIMPLICITY OF THE
$\ast $-SEMISIMPLICITY OF THE 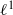 ${\ell }^{1} $-ALGEBRA ON AN ABELIAN
${\ell }^{1} $-ALGEBRA ON AN ABELIAN  $\ast $-SEMIGROUP
$\ast $-SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 15 February 2013, pp. 492-498
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE NATURAL PARTIAL ORDER ON THE SEMIGROUP OF ALL TRANSFORMATIONS OF A SET THAT REFLECT AN EQUIVALENCE RELATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 359-368
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON FREE SPECTRA OF A CLASS OF FINITE INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 07 March 2013, pp. 225-237
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
CENTRALISERS IN THE INFINITE SYMMETRIC INVERSE SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 28 September 2012, pp. 462-479
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
VARIETIES WHOSE TOLERANCES ARE HOMOMORPHIC IMAGES OF THEIR CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 August 2012, pp. 326-338
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Quivers of monoids with basic algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1516-1560
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
ON THE VARIETY GENERATED BY THE MONOID OF TRIANGULAR 2×2 MATRICES OVER A TWO-ELEMENT FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 28 May 2012, pp. 64-77
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
NATURAL PARTIAL ORDER IN SEMIGROUPS OF TRANSFORMATIONS WITH INVARIANT SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 May 2012, pp. 94-107
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
FINITE REGULAR BANDS ARE FINITELY RELATED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1-9
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
A universality result for endomorphism monoids of some ultrahomogeneous structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 635-656
-
- Article
-
- You have access
- Export citation
Gröbner bases for quadratic algebras of skew type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 387-401
-
- Article
-
- You have access
- Export citation
PARTIAL ORDERS ON SEMIGROUPS OF PARTIAL TRANSFORMATIONS WITH RESTRICTED RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 100-118
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
OPTIMAL REES MATRIX CONSTRUCTIONS FOR ANALYSIS OF DATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 08 December 2011, pp. 357-366
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
FREE ADEQUATE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 19 March 2012, pp. 365-390
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
A NEW EXAMPLE OF A MINIMAL NONFINITELY BASED SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 06 September 2011, pp. 484-491
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Retracts of trees and free left adequate semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 17 August 2011, pp. 731-747
-
- Article
-
- You have access
- Export citation
Idempotent-generated semigroups and pseudovarieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 545-568
-
- Article
-
- You have access
- Export citation
PRESENTATIONS OF INVERSE SEMIGROUPS, THEIR KERNELS AND EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 08 July 2011, pp. 289-316
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
COMPLETELY REGULAR MONOIDS WITH TWO GENERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 271-287
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation

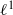

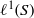

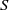

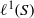


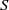
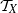
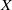
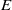
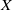
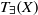
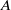
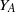
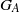
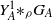
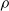
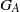
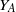
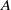
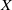
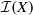
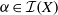
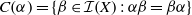

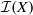
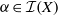
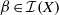
 quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FM
quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FM