Refine listing
Actions for selected content:
285 results in 20Mxx
A NEW CONSTRUCTION FOR REGULAR SEMIGROUPS WITH QUASI-IDEAL ORTHODOX TRANSVERSALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 177-187
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
INJECTIVE TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 327-336
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
On commuting elements and embeddings of graph groups and monoids
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 155-170
-
- Article
-
- You have access
- Export citation
NATURALLY ORDERED TRANSFORMATION SEMIGROUPS PRESERVING AN EQUIVALENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 117-128
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
EMBEDDINGS IN COSET MONOIDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 75-80
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
MODULAR DIOPHANTINE INEQUALITIES AND ROTATIONS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 315-328
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
VARIETIES GENERATED BY COMPLETELY 0-SIMPLE SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 375-403
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
SEMIGROUPS OF LINEAR TRANSFORMATIONS WITH RESTRICTED RANGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 441-453
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
A PROOF OF ISBELL’S ZIGZAG THEOREM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 229-232
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
CANCELLATIVE AND MALCEV PRESENTATIONS FOR FINITE REES INDEX SUBSEMIGROUPS AND EXTENSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 39-61
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
On finite generation and presentability of Schützenberger products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-368
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Canonical Varieties of Completely Regular Semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-104
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
On parabolic submonoids of a class of singular Artin monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-37
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Inverse semigroups determined by their partial automorphism monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-198
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
A property of the complex semigroup algebra of a free monoid
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-104
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Polyhedral convex cones and the equational theory of the bicyclic semigroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 63-96
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Products of idempotents in algebraic monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-203
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Expansions of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 205-228
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Conjugacy in singular Artin monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-212
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
On properties of group closures of one-to-one transformations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 213-229
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
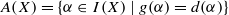 . For example, we describe Green’s relations and ideals in
. For example, we describe Green’s relations and ideals in 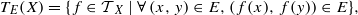
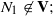 (iii)
(iii) 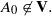 The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.
The conditions (i) and (ii) are also sufficient conditions. In this note, we complete Kublanovsky’s programme by refining condition (iii) to obtain a complete set of conditions that are both necessary and sufficient.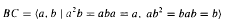 or in the semigroup
or in the semigroup 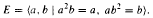 . The semigroups
. The semigroups 