Refine listing
Actions for selected content:
285 results in 20Mxx
Rees matrix semigroups and the regular semidirect product
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 39-60
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Archimedean components of triangular norms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 239-255
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
Completely 0-simple semigroups of left quotients
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-122
- Print publication:
- December 2004
-
- Article
- Export citation
On The Asymptotic Values of Length Functions In Krull And Finitely Generated commutative Monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-436
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Dense subsemigroups of generalised transformation semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 433-446
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
Compact semilattices with open principal filters
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-362
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
A syntactic approach to covers for E-dense semigroups over group varieties
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-245
- Print publication:
- December 2001
-
- Article
- Export citation
Orders in completely regular semigroups
- Part of
-
- Journal:
- Mathematika / Volume 48 / Issue 1-2 / December 2001
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-230
- Print publication:
- December 2001
-
- Article
- Export citation
Semidistributive inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-51
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Remarks concerning finitely generated semigroups having regular sets of unique normal forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 293-310
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Locally full HNN extensions of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-272
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
A note on amalgams of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 71-75
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
The embeddability of ring and semigroup amalgams is undecidable
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 272-286
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
Associativity of the regular semidirect product of existence varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 85-115
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Direct products of automatic semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 19-24
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Inverse semigroups with zero: covers and their structure
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-30
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
On congruence compact monoids
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-224
- Print publication:
- June 1999
-
- Article
- Export citation
Flatness properties of acts over commutative, cancellative monoids
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-102
- Print publication:
- June 1999
-
- Article
- Export citation
Moore-Penrose inversion in complex contracted inverse semigroup algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-302
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Dual symmetric inverse monoids and representation theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-367
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
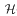 -class of
-class of 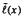 and
and 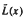 on
on 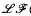 (
(