Refine listing
Actions for selected content:
285 results in 20Mxx
Orders in normal bands of groups
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 2 / December 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 295-319
- Print publication:
- December 1996
-
- Article
- Export citation
Growth of linear semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 18-30
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Regularity and products of idempotents in endomorphism monoids of projective acts
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 2 / December 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 354-367
- Print publication:
- December 1995
-
- Article
- Export citation
Extensions of regular orthogroups by groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 28-60
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Morita equivalence for semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 81-111
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Some remarks on modularity of the congruence lattice of regular ω-semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 54-65
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
On existence varieties of orthodox semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-125
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Artinian band sums of rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 66-72
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
The depth of the semigroup of balanced endomorphisms
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 199-208
- Print publication:
- June 1994
-
- Article
- Export citation
On free products of completely regular semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-231
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Congruence networks for completely simple semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-266
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Congruences on free monoids and submonoids of polycyclic monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 236-253
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Coherent Monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 166-182
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
Semigroups with atomistic congruence lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 88-102
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Totally commutative semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 381-399
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Embedding finite semigroup amalgams
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 489-496
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Duality for distributive bisemilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 247-275
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Hereditary radicals and bands of associative rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 62-72
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
Completely right pure monoids: the general case
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 1 / June 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-88
- Print publication:
- June 1991
-
- Article
- Export citation
The Szendrei expansion of a semigroup
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 251-260
- Print publication:
- December 1990
-
- Article
- Export citation
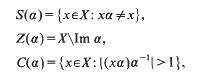
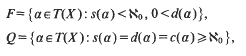
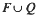 . Furthermore, both
. Furthermore, both 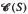 of congruences on a Rees matrix semigroup
of congruences on a Rees matrix semigroup 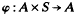 A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right
A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right 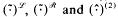 introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4],
introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4], 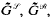
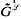 is an
is an 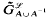 which is a subsemigroup of
which is a subsemigroup of 