We characterize rings whose multiplicative subsemigroups containing 0 and the additive inverse of each element are subrings. In addition we consider commutative rings for which every non-constant multiplicative endormorphism that preserves additive inverses is a ring endomorphism, and we show that they belong to one of three easily-described classes of rings.

Four properties of congruences on a regular semigroup S are studied and compared. Let R, L and D denote Green's relations and let V = {(a, b) ∈ S × S|a and b are mutually inverse}. A congruence ρ on S is (1) rectangular provided ρ ∩ D = (ρ ∩ L) ° (ρ ∩ R), (2) V-commuting provided ρ ° V = V ° ρ, (3) (L, R)-commuting provided L ° ρ = ρ ° L, and R ° ρ = ρ ° R, and (4) idempotent-regular provided each idempotent ρ-class is a regular subsemigroup of S.

A rectangular congruence is (L, R)-commuting and a V-commuting congruence is idempotent-regular. If ρ is idempotent-regular and (L, R)-commuting then ρ is V-commuting. Examples and conditions are given to show what other implications among the four properties hold. In addition to characterizations of the properties, these are studied in the presence of other conditions on S. For example, if S is a stable regular semigroup, then each congruence under D is rectangular.

In this paper “a map” denotes an arbitrary (everywhere defined, or partial, or even multi-valued) mapping. A map is constant if any two elements belonging to its domain have precisely the same images under this map. We characterize those semigroups which can be isomorphic to semigroups of constant maps or to involuted semigroups of constant maps.

A regular semigroup S is said to be locally inverse if each local submonoid eSe, with e an idempotent, is an inverse semigroup. In this paper we apply known covering theorems for inverse semigroups and a covering theorem for locally inverse semigroups due to the author to obtain some covering theorems for locally inverse semigroups. The techniques developed here permit us to give an alternative proof for, and sligbt strengthening of, an important covering theorem for locally inverse semigroups due to F. Pastijn.

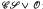If CS(respectively, O) denotes the class of all completely simple semigroups (respectively, semigroups that are orthodox unions of groups) then CS(respectively, O) is a variety of algebras with respect to the operations of multiplication and inversion. The main result shows that the lattice of subvarieties of is a precisely determined subdirect product of the lattice of subvarieties of 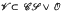CSand the lattice of subvarieties of O. A basis of identities is obtained for any variety in terms of bases of identities for 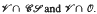. Several operators on the lattice of subvarieties of 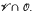are also introduced and studied.

A natural equivalence θ on the lattice of congruences λ(S) of a semigroup S is studied. For any eventually regular semigroup S, it is shown that θ is a congruence, each θ-class is a complete sublattice of λ(S) and the maximum element in each θ-class is determined. 1980 Mathematics subject classification (Amer. Math. Soc.): 20 M 10.

We determine which permutative varieties are saturated and classify all nontrivial permutation identities for the class of all globally idempotent semigroups.

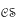Completely simple semigroups form a variety, , of algebras with the operations of multiplication and inversion. It is known that the mapping 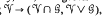, where 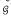is the variety of all groups, is an isomorphism of the lattice 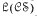of all subvarieties of 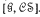onto a subdirect product of the lattice of subvarieties of and the interval . We consider embeddings of into certain direct products on the above pattern with rectangular bands, rectangular groups and central completely simple semigroups in place of groups.

A verbal product is introduced for a particular class of varieties of inverse semigroups and this product is shown to be associative. As well, the structure of this class is examined.

A new arrow notation is used to describe biordered sets. Biordered sets are characterized as biordered subsets of the partial algebras formed by the idempotents of semigroups. Thus it can be shown that in the free semigroup on a biordered set factored out by the equations of the biordered set there is no collapse of idempotents and no new arrows.

We find the atoms of certain subclasses of varieties of finite semigroups and the corresponding varieties of languages. For example we give a new description of languages whose syntactic monoids are R-trivial and idempotent. We also describe the least variety containing all commutative semigroups and at least one non-commutative semigroup. Finally we extend to varieties of finite semigroups some classical results about semilattice decomposition of semigroups.

A variant of Kurosh-Amitsur radical theory is developed for algebras with a collection of (finitary) operations ω, all of which are idempotent, that is satisfy the condition ω(x, x,…, x) = x. In such algebras, all classes of any congruence are subalgebras. In place of a largest normal radical subobject, a largest congruence with radical congruence classes is considered. In congruence-permutable varieties the parallels with conventional radical theory are most striking.

A category V is called universal (or binding) if every category of algebras is isomorphic to a full subcategory of V. The main result states that a semigroup variety V is universal if and only if it contains all commutative semigroups and fails the identity xnyn = (xy)n for every n ≥ 1. Further-more, the universality of a semigroup variety V is equivalent to the existence in V of a nontrivial semigroup whose endomorphism monoid is trivial, and also to the representability of every monoid as the monoid of all endomorphisms of some semigroup in V. Every universal semigroup variety contains a minimal one with this property while there is no smallest universal semigroup variety.

We establish a necessary condition (E) for a semigroup variety to be closed under the taking of epimorphisms and a necessary condition (S) for a variety to consist entirely of saturated semigroups. Condition (S) is shown to be sufficient for heterotypical varieties and a stronger condition (S′) is shown to be sufficient for homotypical varieties.

All inverse semigroups with idempotents dually well-ordered may be constructed inductively. The techniques involved are the constructions of ordinal sums, direct limits and Bruck-Reilly extensions.

Let S be a regular semigroup and A a D(S)-module. We proved in a previous paper that the set Ext(S, A) of equivalence classes of extensions of A by S admits an abelian group structure and studied its functorial properties. The main aim of this paper is to describe Ext(S, A) as a second cohomology group of certain chain complex.

Several morphisms of this lattice V(CR) are found, leading to decompostions of it, and various sublattices, into subdirect products of interval sublattices. For example the map V → V ∪ G (where G is the variety of groups) is shown to be a retraction of V(CR); from modularity of the lattice V(BG) of varieties of bands of groups it follows that the map V → (V ∪ V V G) is an isomorphism of V(BG).

It is shown that a semigroup is right self-injective and a band of groups if and only if it is isomorphic to the spined product of a self-injective semilattice of groups and a right self-injective band. A necessary and sufficient condition for a band to be right self-injective is given. It is shown that a left [right] self-injective semigroup has the [anti-] representation extension property and the right [left] congruence extension property.

Non-completely simple bisimple semigroups S which are generated by a finite number of idempotents are studied by means of Rees matrix semigroups over local submonoids eSe, e = e2 ∈ S. If under the natural partial order on the set Es of idempotents of such a semigroup S the sets ω(e) = {ƒ ∈ Es: ƒ ≤ e} for each e ∈ Es are well-ordered, then S is shown to contain a subsemigroup isomorphic to Sp4, the fundamental four-spiral semigroup. A non-completely simple hisimple semigroup is constructed which is generated by 5 idempotents but which does not contain a subsemigroup isomorphic to Sp4.

Given a universal algebra A, one can define for each positive integer n the set of functions on A which can be “interpolated” at any n elements of A by a polynomial function on A. These sets form a chain with respect to inclusion. It is known for several varieties that many of these sets coincide for all algebras A in the variety. We show here that, in contrast with these results, the coincident sets in the chain can to a large extent be specified arbitrarily by suitably choosing A from the variety of commutative semigroups.