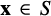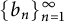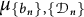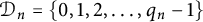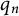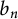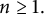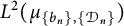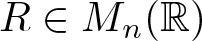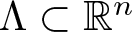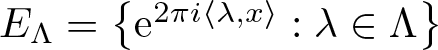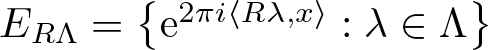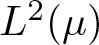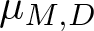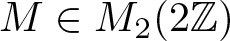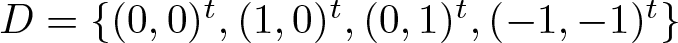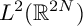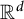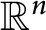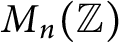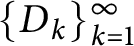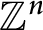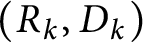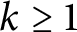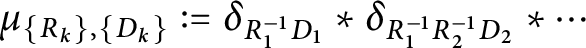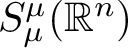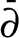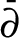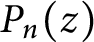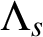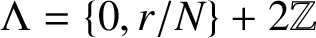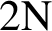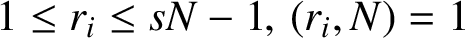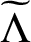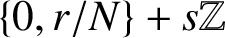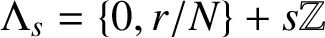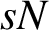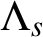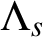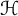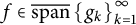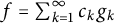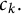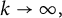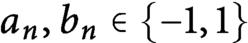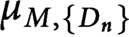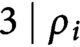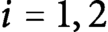Refine listing
Actions for selected content:
82 results in 42Cxx
Study of weaving frames in Krein spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-16
-
- Article
- Export citation
On weaving Hilbert space frames and Riesz bases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1-10
-
- Article
- Export citation
THE SPECTRAL EIGENVALUES OF A CLASS OF PRODUCT-FORM SELF-SIMILAR SPECTRAL MEASURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 246-263
- Print publication:
- October 2025
-
- Article
- Export citation
Superelliptic Affine Lie algebras and orthogonal polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Moment-SOS hierarchy: Applications and related topics
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 841-908
-
- Article
- Export citation
Tree structure of spectra of spectral Moran measures with consecutive digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 593-610
- Print publication:
- September 2024
-
- Article
- Export citation
Truncations of generalized shift-invariant systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 29 November 2023, pp. 504-515
- Print publication:
- June 2024
-
- Article
- Export citation
Remarks on Naimark dilation theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 469-477
- Print publication:
- June 2024
-
- Article
- Export citation
The spectral eigenmatrix problems of planar self-affine measures with four digits
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 897-918
-
- Article
- Export citation
TWISTED SHIFT-INVARIANT SYSTEM IN
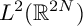 $L^2(\mathbb {R}^{2N})$
$L^2(\mathbb {R}^{2N})$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 251 / September 2023
- Published online by Cambridge University Press:
- 05 June 2023, pp. 734-767
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of exponential bases on union of intervals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1296-1312
- Print publication:
- December 2023
-
- Article
- Export citation
Spectral analysis of bilateral birth–death processes: some new explicit examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 1193-1221
- Print publication:
- December 2022
-
- Article
- Export citation
Spectrality of a class of Moran measures on
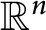 $\mathbb {R}^{n}$ with consecutive digit sets
$\mathbb {R}^{n}$ with consecutive digit sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 269-285
- Print publication:
- March 2023
-
- Article
- Export citation
SPECTRAL INEQUALITIES FOR COMBINATIONS OF HERMITE FUNCTIONS AND NULL-CONTROLLABILITY FOR EVOLUTION EQUATIONS ENJOYING GELFAND–SHILOV SMOOTHING EFFECTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 21 March 2022, pp. 2533-2582
- Print publication:
- November 2023
-
- Article
- Export citation
On smooth perturbations of Chebyshëv polynomials and
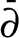 $ \bar {\partial } $-Riemann–Hilbert method
$ \bar {\partial } $-Riemann–Hilbert method
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 February 2022, pp. 142-155
- Print publication:
- March 2023
-
- Article
- Export citation
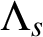 $\Lambda _s$-NONUNIFORM MULTIRESOLUTION ANALYSIS
$\Lambda _s$-NONUNIFORM MULTIRESOLUTION ANALYSIS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 23 November 2021, pp. 359-377
- Print publication:
- June 2023
-
- Article
- Export citation
Extrapolation to weighted Morrey spaces with variable exponents and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 09 November 2021, pp. 1002-1027
-
- Article
- Export citation
Completion versus removal of redundancy by perturbation
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 05 July 2021, pp. 456-465
- Print publication:
- June 2022
-
- Article
- Export citation
Spectrality of Moran Sierpinski-type measures on
 ${\mathbb R}^2$
${\mathbb R}^2$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 1024-1040
- Print publication:
- December 2021
-
- Article
- Export citation
On Pisier’s inequality for UMD targets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 282-291
- Print publication:
- June 2021
-
- Article
- Export citation