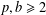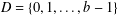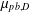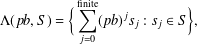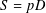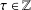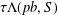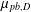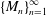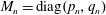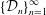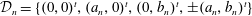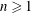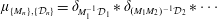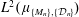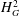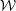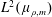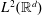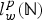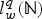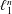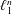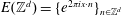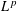Refine listing
Actions for selected content:
82 results in 42Cxx
NUMBER THEORY PROBLEMS RELATED TO THE SPECTRUM OF CANTOR-TYPE MEASURES WITH CONSECUTIVE DIGITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 113-123
- Print publication:
- February 2021
-
- Article
- Export citation
Translates of Functions on the Heisenberg Group and the HRT Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 871-881
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
OPTIMAL LINE PACKINGS FROM FINITE GROUP ACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 January 2020, e6
-
- Article
-
- You have access
- Open access
- Export citation
Spectrality of a Class of Moran Measures
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 17 January 2020, pp. 366-381
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ODD–EVEN DECOMPOSITION OF FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 104-108
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
On Parseval Wavelet Frames via Multiresolution Analyses in
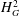 $H_{G}^{2}$
$H_{G}^{2}$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 06 December 2019, pp. 157-172
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
CALDERÓN’S INVERSE PROBLEM WITH A FINITE NUMBER OF MEASUREMENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 October 2019, e35
-
- Article
-
- You have access
- Open access
- Export citation
Non-spectral Problem for Some Self-similar Measures
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 28 August 2019, pp. 318-327
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A Measurable Selector in Kadison’s Carpenter’s Theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 1505-1528
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
On the Gibbs–Wilbraham Phenomenon for Sampling and Interpolatory Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 1163-1171
-
- Article
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation
Lipschitz-free Spaces on Finite Metric Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 February 2019, pp. 774-804
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Three Problems on Exponential Bases
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 55-70
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
ANALYSIS IN THE MULTI-DIMENSIONAL BALL
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 190-212
- Print publication:
- 2019
-
- Article
- Export citation
Stochastic LU factorizations, Darboux transformations and urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 862-886
- Print publication:
- September 2018
-
- Article
- Export citation
A SHORT NOTE ON THE FRAME SET OF ODD FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 481-493
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Hardy-Type Inequalities for Fractional Powers of the Dunkl–Hermite Operator
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 02 April 2018, pp. 513-544
-
- Article
- Export citation
FRAME-LESS HILBERT C*-MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 February 2018, pp. 25-31
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
THE CRAMÉR–WOLD THEOREM ON QUADRATIC SURFACES AND HEISENBERG UNIQUENESS PAIRS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 07 November 2017, pp. 117-135
- Print publication:
- January 2020
-
- Article
- Export citation
Sparse Recovery via ℓq -Minimization for Polynomial Chaos Expansions
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 775-797
- Print publication:
- November 2017
-
- Article
- Export citation