Refine listing
Actions for selected content:
82 results in 42Cxx
The ρ-variation of the heat semigroup in the Hermitian setting: behaviour in L∞
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 569-585
-
- Article
-
- You have access
- Export citation
Expansions with Poisson kernels and related topics
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 153-173
-
- Article
-
- You have access
- Export citation
THE DECAY OF THE WALSH COEFFICIENTS OF SMOOTH FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 430-453
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Quasi-Birth-and-Death Processes, Lattice Path Counting, and Hypergeometric Functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 507-520
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Analytic functions associated with strong Hamburger moment problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 181-187
-
- Article
-
- You have access
- Export citation
ON NEAR EXACT BANACH FRAMES IN BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 335-342
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Extrapolation of the functional calculus of generalized Dirac operators and related embedding and Littlewood-Paley-type theorems. I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-326
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
On a localization property of wavelet coefficients for processes with stationary increments, and applications. I. Localization with respect to shift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 938-962
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Operator-valued multiplier theorems characterizing Hilbert spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-184
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Boundary coiflets for wavelet shrinkage in function estimation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 81-98
- Print publication:
- 2004
-
- Article
- Export citation
Calderón-type reproducing formulae on Lipschitz curves and surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-46
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
The discrete fractional Fourier transform and Harper's equation
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 281-297
- Print publication:
- December 2000
-
- Article
- Export citation
The arithmetic of a semigroup of series of Walsh functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-378
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
Homogeneous solutions of the generalized heat equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 13-45
- Print publication:
- February 1997
-
- Article
-
- You have access
- Export citation
The Appell transform and the semigroup property for temperatures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 109-117
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Asymptotic behaviour of orthogonal polynomials relative to measures with mass points
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 2 / December 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-344
- Print publication:
- December 1993
-
- Article
- Export citation
Evaluation of the decay parameter for some specialized birth-death processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 781-791
- Print publication:
- December 1992
-
- Article
- Export citation
Walsh-Fourier series with coefficients of generalized bounded variation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 458-465
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
Bounded spherical functions for abstract operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 195-203
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
Smoothness conditions and integrability theorems on bounded Vilenkin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 46-61
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
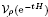 , ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator
, ρ > 2, be the ρ-variation of the heat semigroup associated to the harmonic oscillator 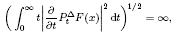
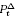 is the classical Poisson kernal in ℝ.
is the classical Poisson kernal in ℝ.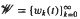 be the classical system of the Walsh functions,
be the classical system of the Walsh functions, 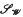 the multiplicative semigroup of the functions represented by series of functions
the multiplicative semigroup of the functions represented by series of functions 