Refine listing
Actions for selected content:
77 results in 57Nxx
Incompressible surfaces and the topology of 3-dimensional manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-22
-
- Article
-
- You have access
- Export citation
Topologically rigid non-Haken 3-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 60-71
-
- Article
-
- You have access
- Export citation
On 4-manifolds with universal covering space a compact geometric manifold
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-148
-
- Article
-
- You have access
- Export citation
Strongly reversible manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 172-176
-
- Article
-
- You have access
- Export citation
Finite group actions on 4-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-296
-
- Article
-
- You have access
- Export citation
Hyperbolic manifolds and degenerating handle additions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 72-89
-
- Article
-
- You have access
- Export citation
On calculation of the Witten invariants of 3-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-398
-
- Article
-
- You have access
- Export citation
Diagrammatically reducible complexes and Haken manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 116-126
-
- Article
-
- You have access
- Export citation
Tameness and geodesic cores of subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-161
-
- Article
-
- You have access
- Export citation
Cusps, triangle groups and hyperbolic 3-folds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
-
- Article
-
- You have access
- Export citation
Quasi-Fuchsian surfaces in hyperbolic knot complements
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 116-131
-
- Article
-
- You have access
- Export citation
Manifolds that fail to be co-dimension 2 fibrators necessarily cover themselves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-68
-
- Article
-
- You have access
- Export citation
Peripheral acyclicity in 3-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 312-321
-
- Article
-
- You have access
- Export citation
h-COBORDISMS AND MAPPING CYLINDER OBSTRUCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 01 April 2009, pp. 249-278
-
- Article
-
- You have access
- Export citation
FINITELY DOMINATED COVERING SPACES OF 3- AND 4-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 99-108
-
- Article
-
- You have access
- Export citation
Integrality of quantum 3-manifold invariants and a rational surgery formula
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1593-1612
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
On estimation of the Euler number by projections of thin slabs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 715-724
- Print publication:
- September 2004
-
- Article
- Export citation
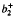 (
(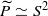 . There is a corresponding result in dimension 4, under further hypotheses on
. There is a corresponding result in dimension 4, under further hypotheses on 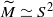 or
or 