Refine listing
Actions for selected content:
327 results in 03CXX
The André–Oort conjecture for the moduli space of abelian surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 2 / February 2013
- Published online by Cambridge University Press:
- 11 December 2012, pp. 204-216
- Print publication:
- February 2013
-
- Article
- Export citation
The algebraic numbers definable in various exponential fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 April 2012, pp. 825-834
- Print publication:
- October 2012
-
- Article
- Export citation
A universality result for endomorphism monoids of some ultrahomogeneous structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 3 / October 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 635-656
-
- Article
-
- You have access
- Export citation
Some unlikely intersections beyond André–Oort
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1-27
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
SOME COVERS AND ENVELOPES IN THE CHAIN COMPLEX CATEGORY OF R-MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 31 August 2011, pp. 385-401
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
SIMPLE EXTENSIONS OF COMBINATORIAL STRUCTURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 193-214
- Print publication:
- July 2011
-
- Article
- Export citation
On stable fields and weight
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 01 July 2010, pp. 349-358
- Print publication:
- April 2011
-
- Article
- Export citation
Elementary theory of valued fields with a valuation-preserving automorphism
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 01 July 2010, pp. 1-35
- Print publication:
- January 2011
-
- Article
- Export citation
Random hypergraphs in pseudofinite fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 03 June 2009, pp. 29-47
- Print publication:
- January 2010
-
- Article
- Export citation
EVERY SHIFT AUTOMORPHISM VARIETY HAS AN INFINITE SUBDIRECTLY IRREDUCIBLE MEMBER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 19 January 2010, pp. 231-238
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Interprétation de l'arithmétique dans certains groupes de permutations affines par morceaux d'un intervalle
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 623-652
- Print publication:
- October 2009
-
- Article
- Export citation
Sur les collapses de corps différentiels colorés en caractéristique nulle décrits par Poizat à l'aide des amalgames à la Hrushovski
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 445-464
- Print publication:
- July 2009
-
- Article
- Export citation
Groupes géométriques de rang de Morley fini
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 751-792
- Print publication:
- October 2008
-
- Article
- Export citation
Some questions concerning Hrushovski's amalgamation constructions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 793-823
- Print publication:
- October 2008
-
- Article
- Export citation
Expansions of fields by angular functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 735-750
- Print publication:
- October 2008
-
- Article
- Export citation
La fusion libre : le cas simple
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 825-868
- Print publication:
- October 2008
-
- Article
- Export citation
Difference fields and descent in algebraic dynamics. I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 653-686
- Print publication:
- October 2008
-
- Article
- Export citation
Difference fields and descent in algebraic dynamics. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 687-704
- Print publication:
- October 2008
-
- Article
- Export citation
Genericity, generosity, and tori
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 705-722
- Print publication:
- October 2008
-
- Article
- Export citation
Questions de corps de définition pour les variétés abéliennes en caractéristique positive
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 623-639
- Print publication:
- October 2008
-
- Article
- Export citation
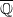 . Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of
. Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of 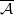 -covers and
-covers and 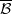 -envelopes of special complexes is considered where
-envelopes of special complexes is considered where 