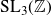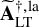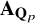Refine listing
Actions for selected content:
603 results in 11Fxx
 $\Omega$-results for exponential sums related to Maass cusp forms for
$\Omega$-results for exponential sums related to Maass cusp forms for 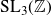 $\mathrm{SL}_3(\mathbb Z)$
$\mathrm{SL}_3(\mathbb Z)$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hybrid subconvexity for Maass form symmetric-square L-functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-51
-
- Article
- Export citation
Conditional lower bounds on the distribution of central values: The case of modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
VORONOI COMPLEXES IN HIGHER DIMENSIONS, COHOMOLOGY OF
 $GL_N(\mathbb{Z} )$ FOR
$GL_N(\mathbb{Z} )$ FOR  $N\geqslant 8$ AND THE TRIVIALITY OF
$N\geqslant 8$ AND THE TRIVIALITY OF  $K_8(\mathbb{Z} )$
$K_8(\mathbb{Z} )$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-26
-
- Article
- Export citation
NON-SEMI-STABLE LOCI IN HECKE STACKS AND FARGUES’ CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher power sums of Fourier coefficients of symmetric square L-functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 October 2025, pp. 1-22
-
- Article
- Export citation
The dual pair
 $\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
$\mathrm {Aut}(C)\times F_{4}$ (p-adic case)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 October 2025, e174
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locally analytic vectors and decompletion in mixed characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 October 2025, e173
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subspaces spanned by eigenforms with nonvanishing twisted central L-values
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigid meromorphic cocycles for orthogonal groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit spectral gap for Hecke congruence covers of arithmetic Schottky surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 26 September 2025, pp. 1-41
-
- Article
- Export citation
Klingen Eisenstein congruences and modularity
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On moments of L-functions over Dirichlet characters
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-24
-
- Article
- Export citation
Improved bounds for Serre’s open image theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-19
-
- Article
- Export citation
Cycles relations in the affine Grassmannian and applications to the Breuil–Mézard conjecture for G-crystalline representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 03 November 2025, pp. 2320-2372
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-adic interpolation of Gauss–Manin connections on nearly overconvergent modular forms and p-adic L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 05 November 2025, pp. 2380-2441
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic formula for shifted convolution sums involving the coefficients of an L-function
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-20
-
- Article
- Export citation
K3 SURFACES AND ORTHOGONAL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 29 August 2025, pp. 687-727
- Print publication:
- December 2025
-
- Article
- Export citation
Unimodular Hunting II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Murmurations of modular forms and p-power coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 180 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 26 August 2025, pp. 65-92
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation