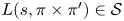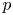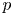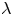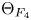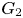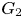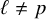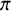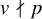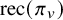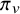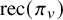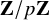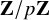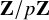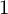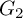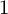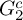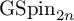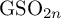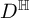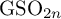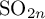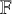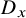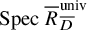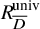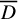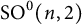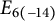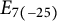Refine listing
Actions for selected content:
600 results in 11Fxx
Zeros of Rankin–Selberg L-functions in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1041-1072
- Print publication:
- May 2024
-
- Article
- Export citation
NONDEFINABILITY RESULTS FOR ELLIPTIC AND MODULAR FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy of rational points in simple algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 13 March 2024, pp. 836-877
- Print publication:
- April 2024
-
- Article
- Export citation
The sup-norm problem beyond the newform
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Components of moduli stacks of two-dimensional Galois representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
There are at most finitely many singular moduli that are S-units
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 732-770
- Print publication:
- April 2024
-
- Article
- Export citation
Moments of the central L-values of the Asai lifts
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 796-804
- Print publication:
- September 2024
-
- Article
- Export citation
Modular forms of half-integral weight on exceptional groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 22 February 2024, pp. 657-707
- Print publication:
- March 2024
-
- Article
- Export citation
Local-global compatibility for regular algebraic cuspidal automorphic representations when
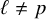 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 12 February 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irregular cusps of orthogonal modular varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 February 2024, pp. 739-769
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES FOR RANKS OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 280-290
- Print publication:
- October 2024
-
- Article
- Export citation
Smith theory and cyclic base change functoriality
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of trianguline Galois representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING DISCRETE, LEVEL-
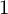 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 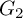 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GALOIS REPRESENTATIONS FOR EVEN GENERAL SPECIAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 1959-2050
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slopes in eigenvarieties for definite unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 52-89
- Print publication:
- January 2024
-
- Article
- Export citation
Equidimensionality of universal pseudodeformation rings in characteristic p for absolute Galois groups of p-adic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein congruences among Euler systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 425-446
- Print publication:
- June 2024
-
- Article
- Export citation
On local Galois deformation rings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 October 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation