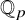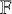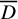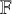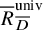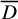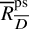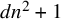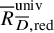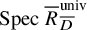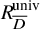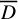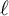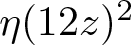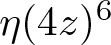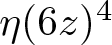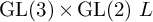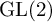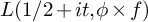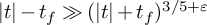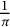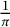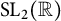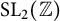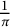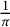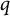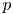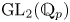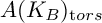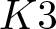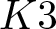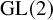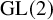Refine listing
Actions for selected content:
604 results in 11Fxx
Equidimensionality of universal pseudodeformation rings in characteristic p for absolute Galois groups of p-adic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eisenstein congruences among Euler systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 425-446
- Print publication:
- June 2024
-
- Article
- Export citation
On local Galois deformation rings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 October 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isogeny graphs on superspecial abelian varieties: eigenvalues and connection to Bruhat–Tits buildings
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1891-1916
- Print publication:
- December 2024
-
- Article
- Export citation
The Local Langlands Conjecture for
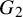 $G_2$
$G_2$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 October 2023, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the vanishing of the coefficients of CM eta quotients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 1202-1216
-
- Article
- Export citation
UNIFORM BOUNDS FOR
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1607-1650
- Print publication:
- July 2024
-
- Article
- Export citation
GENERALISED AUTOMORPHIC SHEAVES AND THE PROPORTIONALITY PRINCIPLE OF HIRZEBRUCH-MUMFORD
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 10 October 2023, pp. 1567-1605
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Concentration of closed geodesics in the homology of modular curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ramanujan-type series for
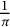 $\frac {1}{\pi }$, revisited
$\frac {1}{\pi }$, revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 350-368
- Print publication:
- June 2024
-
- Article
- Export citation
The Kudla–Millson form via the Mathai–Quillen formalism
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 1638-1663
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the étale cohomology of Hilbert modular varieties with torsion coefficients
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2279-2325
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois groups and prime divisors in random quadratic sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hodge classes and the Jacquet–Langlands correspondence
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 06 September 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An approximation formula for the shifted cubic moment of automorphic L-functions in the weight aspect
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 06 September 2023, pp. 715-738
- Print publication:
- June 2025
-
- Article
- Export citation
ON THE ESSENTIAL TORSION FINITENESS OF ABELIAN VARIETIES OVER TORSION FIELDS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 91-127
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New mock theta functions and formulas for basic hypergeometric series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 868-896
-
- Article
- Export citation
Exact formulae and Turán inequalities for Vafa–Witten invariants of
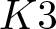 $K3$ surfaces
$K3$ surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 845-861
-
- Article
- Export citation
Exotic Monoidal Structures and Abstractly Automorphic Representations for
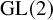 $\mathrm {GL}(2)$
$\mathrm {GL}(2)$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 August 2023, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation