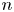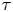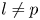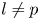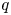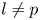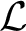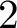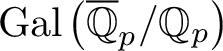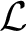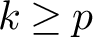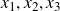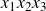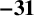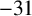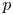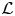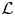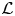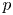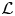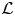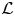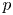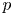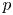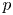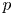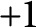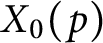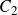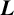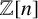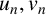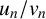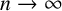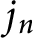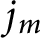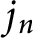Refine listing
Actions for selected content:
604 results in 11Fxx
On the algebraicity about the Hodge numbers of the Hilbert schemes of algebraic surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 392-403
-
- Article
- Export citation
ON A PROPERNESS OF THE HILBERT EIGENVARIETY AT INTEGRAL WEIGHTS: THE CASE OF QUADRATIC RESIDUE FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 08 April 2022, pp. 2645-2716
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic local deformation rings when
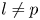 $l \neq p$
$l \neq p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 721-749
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REDUCTIONS OF
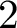 $2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE
$2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE 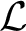 $\mathcal L$-INVARIANT
$\mathcal L$-INVARIANT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 01 April 2022, pp. 2619-2644
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTREME VALUES OF THE RANKIN–SELBERG
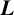 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 408-418
- Print publication:
- December 2022
-
- Article
- Export citation
Uniform bounds for norms of theta series and arithmetic applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 669-691
- Print publication:
- November 2022
-
- Article
- Export citation
LOWER-ORDER TERMS OF THE ONE-LEVEL DENSITY OF A FAMILY OF QUADRATIC HECKE
 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 178-221
- Print publication:
- April 2023
-
- Article
- Export citation
THE p-ADIC GROSS–ZAGIER FORMULA ON SHIMURA CURVES, II: NONSPLIT PRIMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 February 2022, pp. 2199-2240
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Packable hyperbolic surfaces with symmetries
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 February 2022, pp. 103-113
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN APPLICATION OF BINARY QUADRATIC FORMS OF DISCRIMINANT
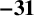 $\boldsymbol {-31}$ TO MODULAR FORMS
$\boldsymbol {-31}$ TO MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 269-272
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Big principal series,
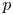 $p$-adic families and
$p$-adic families and 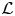 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 409-436
- Print publication:
- February 2022
-
- Article
- Export citation
The spectral p-adic Jacquet–Langlands correspondence and a question of Serre
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 11 April 2022, pp. 245-286
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion properties of modified diagonal classes on triple products of modular curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 68-86
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On combinatorics of the Arthur trace formula, convex polytopes, and toric varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 375-420
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wild Galois representations: a family of hyperelliptic curves with large inertia image
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 619-633
- Print publication:
- November 2022
-
- Article
- Export citation
N-colored generalized Frobenius partitions: generalized Kolitsch identities
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 447-469
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING HECKE EIGENFORMS WITH NONVANISHING
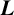 $\boldsymbol {L}$-VALUE
$\boldsymbol {L}$-VALUE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 28-47
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APÉRY LIMITS FOR ELLIPTIC
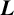 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stieltjes interlacing of the zeros of
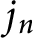 $j_n$
$j_n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 January 2022, pp. 976-993
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A FREENESS CRITERION WITHOUT PATCHING FOR MODULES OVER LOCAL RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 20 December 2021, pp. 2117-2129
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation