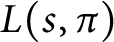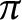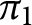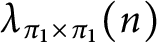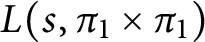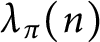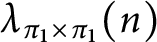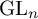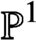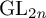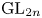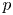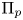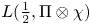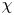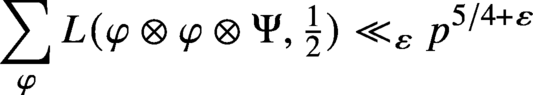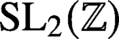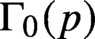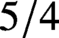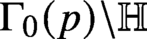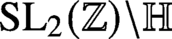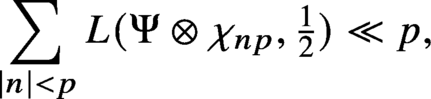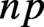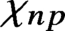Refine listing
Actions for selected content:
599 results in 11Fxx
Cancellation of two classes of dirichlet coefficients over Beatty sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 234-252
- Print publication:
- March 2022
-
- Article
- Export citation
HECKE OPERATORS AND THE COHERENT COHOMOLOGY OF SHIMURA VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 April 2021, pp. 1-69
- Print publication:
- January 2023
-
- Article
- Export citation
R-GROUP AND WHITTAKER SPACE OF SOME GENUINE REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2021, pp. 213-273
- Print publication:
- January 2023
-
- Article
- Export citation
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 03 March 2021, pp. 2001-2041
- Print publication:
- November 2022
-
- Article
- Export citation
Overconvergent modular forms are highest-weight vectors in the Hodge-Tate weight zero part of completed cohomology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 02 March 2021, e17
-
- Article
-
- You have access
- Open access
- Export citation
Eigenfunctions of the Fourier transform with specified zeros
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 329-367
- Print publication:
- September 2021
-
- Article
- Export citation
RAISING THE LEVEL OF AUTOMORPHIC REPRESENTATIONS OF
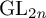 $\mathrm {GL}_{2n}$ OF UNITARY TYPE
$\mathrm {GL}_{2n}$ OF UNITARY TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1421-1444
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
KODAIRA DIMENSION OF UNIVERSAL HOLOMORPHIC SYMPLECTIC VARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 1849-1866
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Le transfert singulier pour la formule des traces de Jacquet–Rallis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 16 March 2021, pp. 303-434
- Print publication:
- February 2021
-
- Article
- Export citation
Curves on K3 surfaces in divisibility 2
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e9
-
- Article
-
- You have access
- Open access
- Export citation
IHARA LEMMA AND LEVEL RAISING IN HIGHER DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1701-1726
- Print publication:
- September 2022
-
- Article
- Export citation
THE COHOMOLOGY OF UNRAMIFIED RAPOPORT–ZINK SPACES OF EL-TYPE AND HARRIS’S CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 14 January 2021, pp. 1163-1218
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- Export citation
The second moment of symmetric square L-functions over Gaussian integers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 January 2021, pp. 54-80
- Print publication:
- February 2022
-
- Article
- Export citation
ON A CERTAIN LOCAL IDENTITY FOR LAPID–MAO’S CONJECTURE AND FORMAL DEGREE CONJECTURE : EVEN UNITARY GROUP CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1107-1161
- Print publication:
- July 2022
-
- Article
- Export citation
EXTREME VALUES OF GEODESIC PERIODS ON ARITHMETIC HYPERBOLIC SURFACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 December 2020, pp. 1507-1542
- Print publication:
- September 2022
-
- Article
- Export citation
On a conjecture of Chen and Yui: Resultants and discriminants
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 14 December 2020, pp. 486-526
- Print publication:
- April 2022
-
- Article
- Export citation
L-functions of GL2n: p-adic properties and non-vanishing of twists
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 08 January 2021, pp. 2437-2468
- Print publication:
- December 2020
-
- Article
- Export citation
Directions in orbits of geometrically finite hyperbolic subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 23 November 2020, pp. 277-316
- Print publication:
- September 2021
-
- Article
- Export citation
Profinite invariants of arithmetic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e54
-
- Article
-
- You have access
- Open access
- Export citation
Bounds for twisted symmetric square L-functions via half-integral weight periods
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e44
-
- Article
-
- You have access
- Open access
- Export citation