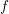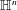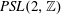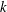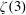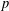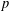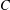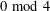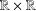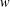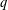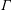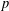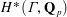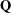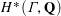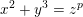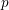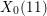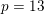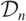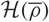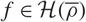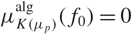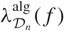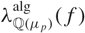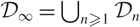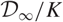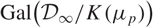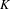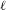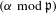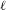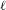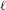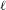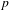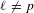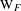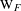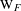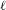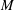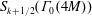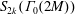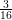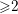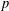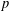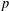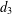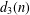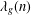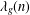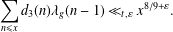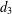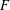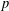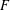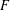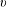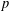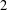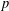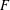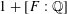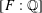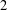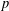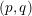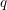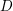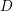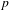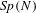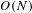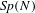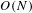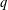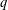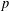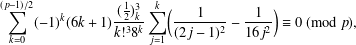Refine listing
Actions for selected content:
599 results in 11Fxx
Ordinary primes in Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 06 February 2020, pp. 647-678
- Print publication:
- April 2020
-
- Article
- Export citation
Ideal Uniform Polyhedra in
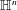 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
COMPARISON OF LOCAL RELATIVE CHARACTERS AND THE ICHINO–IKEDA CONJECTURE FOR UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1803-1854
- Print publication:
- November 2021
-
- Article
- Export citation
ON THE EXISTENCE OF ADMISSIBLE SUPERSINGULAR REPRESENTATIONS OF
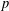 $p$-ADIC REDUCTIVE GROUPS
$p$-ADIC REDUCTIVE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
RANK GENERATING FUNCTIONS FOR ODD-BALANCED UNIMODAL SEQUENCES, QUANTUM JACOBI FORMS, AND MOCK JACOBI FORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 157-175
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
DERIVED HECKE ALGEBRA AND COHOMOLOGY OF ARITHMETIC GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 23 December 2019, e7
-
- Article
-
- You have access
- Open access
- Export citation
The generalized Fermat equation with exponents 2, 3,
 $n$
$n$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 77-113
- Print publication:
- January 2020
-
- Article
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
Variation of the algebraic λ-invariant over a solvable extension
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 21 November 2019, pp. 499-521
- Print publication:
- May 2021
-
- Article
- Export citation
REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1637-1669
- Print publication:
- September 2021
-
- Article
- Export citation
THE
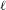 $\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS
$\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 1585-1635
- Print publication:
- September 2021
-
- Article
- Export citation
Newforms of Half-integral Weight: The Minus Space Counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 31 October 2019, pp. 326-372
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On Selberg’s eigenvalue conjecture for moduli spaces of abelian differentials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 30 October 2019, pp. 2354-2398
- Print publication:
- December 2019
-
- Article
- Export citation
EISENSTEIN–KRONECKER SERIES VIA THE POINCARÉ BUNDLE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 30 September 2019, e34
-
- Article
-
- You have access
- Open access
- Export citation
A SHIFTED CONVOLUTION SUM OF
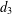 $d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
$d_{3}$ AND THE FOURIER COEFFICIENTS OF HECKE–MAASS FORMS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 26 September 2019, pp. 401-414
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
PARALLEL WEIGHT 2 POINTS ON HILBERT MODULAR EIGENVARIETIES AND THE PARITY CONJECTURE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 September 2019, e27
-
- Article
-
- You have access
- Open access
- Export citation
On some incomplete theta integrals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 9 / September 2019
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1711-1746
- Print publication:
- September 2019
-
- Article
- Export citation
A COMBINATORIAL SOLUTION TO MŒGLIN’S PARAMETRIZATION OF ARTHUR PACKETS FOR
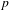 $p$-ADIC QUASISPLIT
$p$-ADIC QUASISPLIT 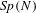 $Sp(N)$ AND
$Sp(N)$ AND 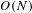 $O(N)$
$O(N)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 25 July 2019, pp. 1091-1204
- Print publication:
- July 2021
-
- Article
- Export citation
DEFORMATION CONDITIONS FOR PSEUDOREPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 18 July 2019, e20
-
- Article
-
- You have access
- Open access
- Export citation
A
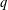 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 294-298
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation