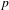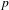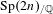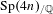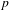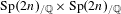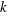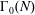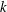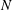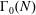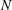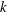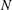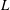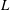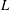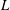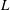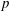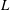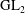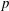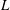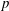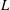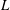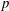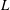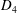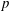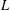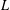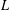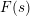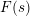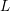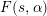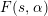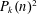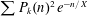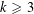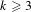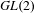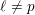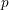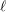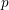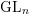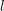Refine listing
Actions for selected content:
599 results in 11Fxx
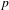 $p$-ADIC
$p$-ADIC  $L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
$L$-FUNCTIONS FOR ORDINARY FAMILIES ON SYMPLECTIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 1287-1347
- Print publication:
- July 2020
-
- Article
- Export citation
Eisenstein Series Arising from Jordan Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 183-201
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Factorization Tests and Algorithms Arising from Counting Modular Forms and Automorphic Representations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 81-97
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Weighted Distribution of Low-lying Zeros of GL(2)
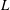 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 08 January 2019, pp. 153-182
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Models of Representations and Langlands Functoriality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 676-707
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
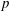 $p$-adic
$p$-adic 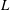 $L$-functions for
$L$-functions for 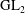 $\text{GL}_{2}$
$\text{GL}_{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1019-1059
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Irregular Weight One Points with
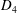 $D_{4}$ Image
$D_{4}$ Image
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 109-118
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
A CONVERSE THEOREM WITHOUT ROOT NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 862-873
- Print publication:
- 2019
-
- Article
- Export citation
QUANTITATIVE ESTIMATES FOR SIMPLE ZEROS OF
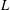 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 375-399
- Print publication:
- 2019
-
- Article
- Export citation
ON A TWISTED VERSION OF LINNIK AND SELBERG’S CONJECTURE ON SUMS OF KLOOSTERMAN SUMS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 437-474
- Print publication:
- 2019
-
- Article
- Export citation
A MEAN VALUE RESULT FOR A PRODUCT OF GL(2) AND GL(3)
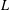 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 743-762
- Print publication:
- 2019
-
- Article
- Export citation
A CERTAIN DIRICHLET SERIES OF RANKIN–SELBERG TYPE ASSOCIATED WITH THE IKEDA LIFT OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 17 June 2019, pp. 897-928
- Print publication:
- 2019
-
- Article
- Export citation
HYPERGEOMETRIC MODULAR EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 338-366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Open access
- Export citation
ON THE STANDARD TWIST OF THE
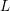 $L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
$L$-FUNCTIONS OF HALF-INTEGRAL WEIGHT CUSP FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 150-180
- Print publication:
- December 2020
-
- Article
- Export citation
ON SOME NEW MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 53-66
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
SECOND MOMENTS IN THE GENERALIZEDGAUSS CIRCLE PROBLEM
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 19 December 2018, e24
-
- Article
-
- You have access
- Open access
- Export citation
EULER SYSTEMS FOR HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 15 November 2018, e23
-
- Article
-
- You have access
- Open access
- Export citation
SYMMETRIC POWER CONGRUENCE IDEALS AND SELMER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 14 November 2018, pp. 1521-1572
- Print publication:
- September 2020
-
- Article
- Export citation
BEYOND ENDOSCOPY VIA THE TRACE FORMULA – IIITHE STANDARD REPRESENTATION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1349-1387
- Print publication:
- July 2020
-
- Article
- Export citation
Minimally ramified deformations when
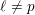 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 1-37
- Print publication:
- January 2019
-
- Article
- Export citation