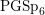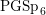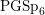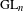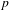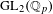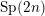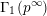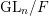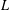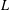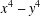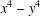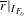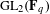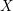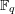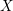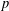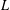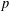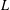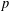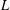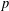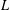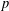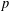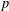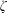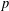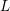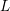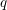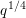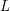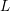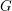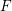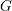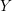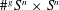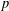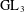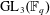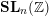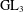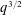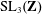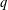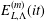Refine listing
Actions for selected content:
599 results in 11Fxx
An exceptional Siegel–Weil formula and poles of the Spin L-function of
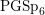 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1231-1261
- Print publication:
- June 2020
-
- Article
- Export citation
A CLASS OF NONHOLOMORPHIC MODULAR FORMS II: EQUIVARIANT ITERATED EISENSTEIN INTEGRALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 28 May 2020, e31
-
- Article
-
- You have access
- Open access
- Export citation
PATCHING AND THE COMPLETED HOMOLOGY OF LOCALLY SYMMETRIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 27 May 2020, pp. 395-458
- Print publication:
- March 2022
-
- Article
- Export citation
Shimura varieties at level
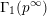 $\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
$\unicode[STIX]{x1D6E4}_{1}(p^{\infty })$ and Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 26 May 2020, pp. 1152-1230
- Print publication:
- June 2020
-
- Article
- Export citation
PERIOD IDENTITIES OF CM FORMS ON QUATERNION ALGEBRAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 May 2020, e25
-
- Article
-
- You have access
- Open access
- Export citation
INTEGERS REPRESENTED BY
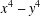 $x^{4}-y^{4}$ REVISITED
$x^{4}-y^{4}$ REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 38-49
- Print publication:
- February 2021
-
- Article
- Export citation
MULTIPLICITY ONE AT FULL CONGRUENCE LEVEL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 15 May 2020, pp. 637-658
- Print publication:
- March 2022
-
- Article
- Export citation
Cuspidal cohomology of stacks of shtukas
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1079-1151
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
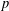 $p$-ADIC
$p$-ADIC 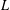 $L$-FUNCTIONS FOR UNITARY GROUPS
$L$-FUNCTIONS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 May 2020, e9
-
- Article
-
- You have access
- Open access
- Export citation
ON THE IRREDUCIBLE COMPONENTS OF SOME CRYSTALLINE DEFORMATION RINGS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 April 2020, e22
-
- Article
-
- You have access
- Open access
- Export citation
Motohashi’s fourth moment identity for non-archimedean test functions and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 1004-1038
- Print publication:
- May 2020
-
- Article
- Export citation
Lower bounds for Maass forms on semisimple groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 959-1003
- Print publication:
- May 2020
-
- Article
- Export citation
Local Rankin–Selberg integrals for Speh representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 13 April 2020, pp. 908-945
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE COHOMOLOGY OF TORELLI GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 April 2020, e7
-
- Article
-
- You have access
- Open access
- Export citation
The Modularity of Special Cycles on Orthogonal Shimura Varieties over Totally Real Fields under the Beilinson–Bloch Conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 March 2020, pp. 39-53
- Print publication:
- March 2021
-
- Article
- Export citation
VANISHING COEFFICIENTS IN QUOTIENTS OF THETA FUNCTIONS OF MODULUS FIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 27 March 2020, pp. 387-398
- Print publication:
- December 2020
-
- Article
- Export citation
SERRE WEIGHTS AND BREUIL’S LATTICE CONJECTURE IN DIMENSION THREE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 25 March 2020, e5
-
- Article
-
- You have access
- Open access
- Export citation
Stability in the high-dimensional cohomology of congruence subgroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 822-861
- Print publication:
- April 2020
-
- Article
- Export citation
PERIODIC TWISTS OF
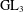 $\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
$\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 12 March 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 118-125
- Print publication:
- August 2020
-
- Article
-
- You have access
- Open access
- Export citation