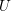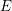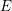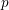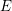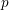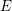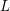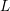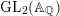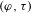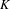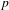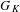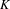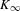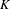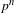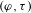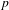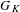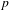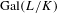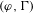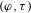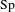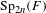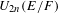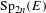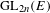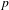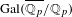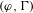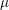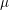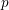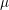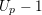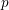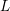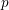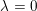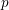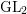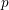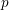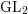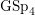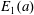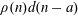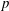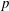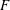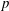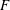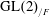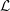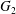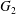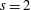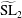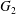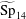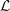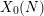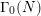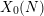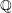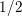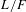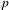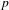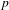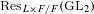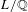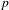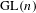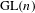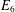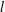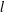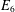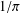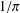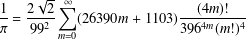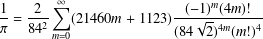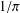Refine listing
Actions for selected content:
599 results in 11Fxx
Families of Picard modular forms and an application to the Bloch–Kato conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1327-1401
- Print publication:
- July 2019
-
- Article
- Export citation
ON LOCAL FIELDS GENERATED BY DIVISION VALUES OF FORMAL DRINFELD MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 14 June 2019, pp. 459-472
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Simple zeros of automorphic
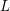 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 30 May 2019, pp. 1224-1243
- Print publication:
- June 2019
-
- Article
- Export citation
LOCALLY ANALYTIC VECTORS AND OVERCONVERGENT
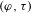 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D70F})$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 May 2019, pp. 137-185
- Print publication:
- January 2021
-
- Article
- Export citation
ON
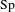 $\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS
$\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 17 April 2019, pp. 225-276
- Print publication:
- January 2021
-
- Article
- Export citation
COHOMOLOGY AND OVERCONVERGENCE FOR REPRESENTATIONS OF POWERS OF GALOIS GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 11 April 2019, pp. 361-421
- Print publication:
- March 2021
-
- Article
- Export citation
Congruences with Eisenstein series and
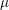 $\unicode[STIX]{x1D707}$-invariants
$\unicode[STIX]{x1D707}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 863-901
- Print publication:
- May 2019
-
- Article
- Export citation
Galois level and congruence ideal for
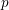 $p$-adic families of finite slope Siegel modular forms
$p$-adic families of finite slope Siegel modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 27 March 2019, pp. 776-831
- Print publication:
- April 2019
-
- Article
- Export citation
Chebyshev’s bias for analytic L-functions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 22 March 2019, pp. 103-140
- Print publication:
- July 2020
-
- Article
- Export citation
VANISHING COEFFICIENTS IN FOUR QUOTIENTS OF INFINITE PRODUCT EXPANSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 216-224
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
The Bombieri–Vinogradov Theorem on Higher Rank Groups and its Applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 928-966
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Ramification of the Eigencurve at Classical RM Points
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 07 March 2019, pp. 57-88
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Poles of the Standard
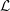 ${\mathcal{L}}$-function of
${\mathcal{L}}$-function of 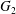 $G_{2}$ and the Rallis–Schiffmann Lift
$G_{2}$ and the Rallis–Schiffmann Lift
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 1127-1161
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A CONVERSE THEOREM FOR BORCHERDS PRODUCTS ON
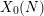 $X_{0}(N)$
$X_{0}(N)$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 01 March 2019, pp. 237-256
- Print publication:
- December 2020
-
- Article
- Export citation
TWISTED TRIPLE PRODUCT
 $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
$\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 20 February 2019, pp. 1947-1992
- Print publication:
- November 2020
-
- Article
- Export citation
PARITY OF THE LANGLANDS PARAMETERS OF CONJUGATE SELF-DUAL REPRESENTATIONS OF
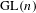 $\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
$\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 February 2019, pp. 2017-2043
- Print publication:
- November 2020
-
- Article
- Export citation
A MAGNETIC DOUBLE INTEGRAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 9-25
- Print publication:
- August 2019
-
- Article
-
- You have access
- Open access
- Export citation
COMPATIBLE SYSTEMS OF GALOIS REPRESENTATIONS ASSOCIATED TO THE EXCEPTIONAL GROUP
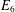 $E_{6}$
$E_{6}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 06 February 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
A MODULAR PROOF OF TWO OF RAMANUJAN’S FORMULAE FOR
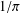 $1/\unicode[STIX]{x1D70B}$
$1/\unicode[STIX]{x1D70B}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 131-144
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The fifth moment of Hecke L-functions in the weight aspect
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 168 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 14 January 2019, pp. 543-566
- Print publication:
- May 2020
-
- Article
- Export citation