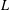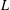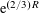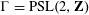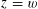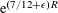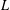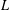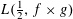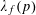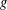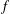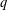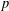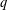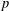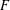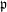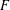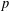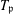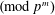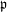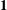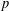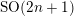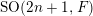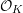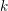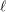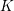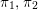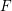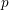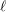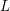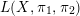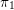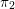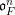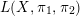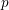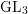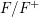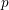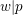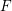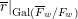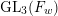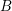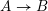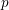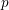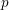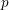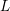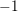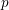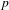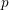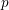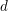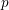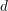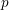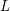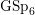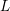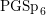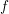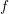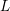Refine listing
Actions for selected content:
599 results in 11Fxx
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 07 February 2018, pp. 184-210
- Print publication:
- 2018
-
- Article
- Export citation
LOCAL AVERAGE OF THE HYPERBOLIC CIRCLE PROBLEM FOR FUCHSIAN GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 1 / 2018
- Published online by Cambridge University Press:
- 06 February 2018, pp. 159-183
- Print publication:
- 2018
-
- Article
- Export citation
LEVEL RECIPROCITY IN THE TWISTED SECOND MOMENT OF RANKIN–SELBERG
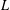 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 26 June 2018, pp. 770-784
- Print publication:
- 2018
-
- Article
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ARISING FROM HILBERT MODULAR SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 23 November 2017, e29
-
- Article
-
- You have access
- Open access
- Export citation
A MODULI INTERPRETATION FOR THE NON-SPLIT CARTAN MODULAR CURVE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 411-434
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
LOCAL BORCHERDS PRODUCTS FOR UNITARY GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 27 October 2017, pp. 139-169
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
Nearby cycles of automorphic étale sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 05 October 2017, pp. 80-119
- Print publication:
- January 2018
-
- Article
- Export citation
The Schwarzian equation for completely replicable functions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 20 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 01 October 2017, pp. 30-52
-
- Article
-
- You have access
- Export citation
REPRÉSENTATIONS DE RÉDUCTION UNIPOTENTE POUR
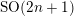 $\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
$\operatorname{SO}(2n+1)$, II : ENDOSCOPIE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 21 September 2017, pp. 87-154
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
Good reduction of K3 surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 18 September 2017, pp. 1-35
- Print publication:
- January 2018
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TEST VECTORS FOR LOCAL CUSPIDAL RANKIN–SELBERG INTEGRALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 12 September 2017, pp. 170-192
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
On mod
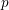 $p$ local-global compatibility for
$p$ local-global compatibility for 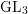 $\text{GL}_{3}$ in the ordinary case
$\text{GL}_{3}$ in the ordinary case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 25 August 2017, pp. 2215-2286
- Print publication:
- November 2017
-
- Article
- Export citation
Proof of de Smit’s conjecture: a freeness criterion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2310-2317
- Print publication:
- November 2017
-
- Article
- Export citation
The
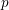 $p$ -adic Gross–Zagier formula on Shimura curves
$p$ -adic Gross–Zagier formula on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 11 July 2017, pp. 1987-2074
- Print publication:
- October 2017
-
- Article
- Export citation
WHITTAKER FUNCTIONS AND DEMAZURE CHARACTERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 June 2017, pp. 759-781
- Print publication:
- July 2019
-
- Article
- Export citation
Explicit Serre weights for two-dimensional Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1893-1907
- Print publication:
- September 2017
-
- Article
- Export citation
Automorphic products of singular weight
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 1855-1892
- Print publication:
- September 2017
-
- Article
- Export citation
Minimal weights of Hilbert modular forms in characteristic
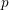 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 9 / September 2017
- Published online by Cambridge University Press:
- 13 June 2017, pp. 1769-1778
- Print publication:
- September 2017
-
- Article
- Export citation
The spin
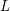 $L$ -function on
$L$ -function on 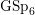 $\text{GSp}_{6}$ for Siegel modular forms
$\text{GSp}_{6}$ for Siegel modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 10 May 2017, pp. 1391-1432
- Print publication:
- July 2017
-
- Article
- Export citation
THE DOUBLE SHUFFLE RELATIONS FOR MULTIPLE EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 180-212
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation