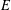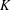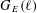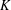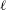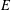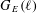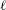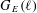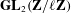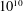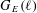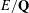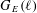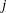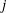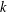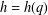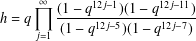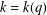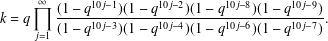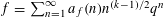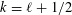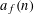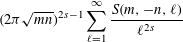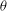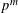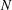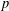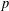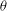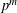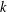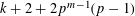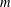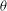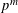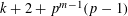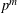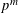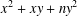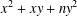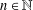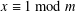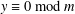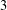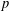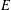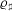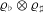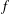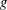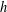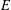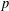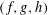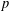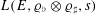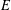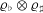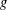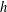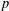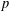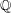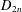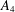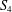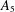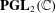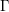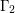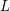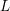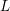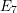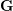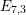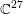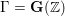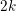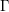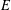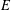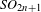Refine listing
Actions for selected content:
599 results in 11Fxx
COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
Real-dihedral harmonic Maass forms and CM-values of Hilbert modular functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 1159-1197
- Print publication:
- June 2016
-
- Article
- Export citation
THE LEVEL 12 ANALOGUE OF RAMANUJAN’S FUNCTION
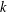 $k$
$k$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 29-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
ON SIGN CHANGES FOR ALMOST PRIME COEFFICIENTS OF HALF-INTEGRAL WEIGHT MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 06 May 2016, pp. 801-810
- Print publication:
- 2016
-
- Article
- Export citation
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 28 January 2016, pp. 406-429
- Print publication:
- 2016
-
- Article
- Export citation
ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 321-336
- Print publication:
- 2016
-
- Article
- Export citation
SIGN OF FOURIER COEFFICIENTS OF MODULAR FORMS OF HALF-INTEGRAL WEIGHT
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 866-883
- Print publication:
- 2016
-
- Article
- Export citation
REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM
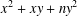 $x^{2}+xy+ny^{2}$
$x^{2}+xy+ny^{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 182-191
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Ramanujan's Radial Limits and Mixed Mock Modular Bilateral q-Hypergeometric Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 26 October 2015, pp. 787-799
-
- Article
- Export citation
PERIODS OF AUTOMORPHIC FORMS: THE TRILINEAR CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 26 October 2015, pp. 59-74
- Print publication:
- February 2018
-
- Article
- Export citation
STARK POINTS AND
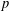 $p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
$p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 13 October 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation
KUDLA’S MODULARITY CONJECTURE AND FORMAL FOURIER–JACOBI SERIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 01 October 2015, e7
-
- Article
-
- You have access
- Open access
- Export citation
ON THE LOCAL LANGLANDS CORRESPONDENCE FOR SPLIT CLASSICAL GROUPS OVER LOCAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 987-1074
- Print publication:
- November 2017
-
- Article
- Export citation
The Chowla–Selberg formula for abelian CM fields and Faltings heights
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 445-476
- Print publication:
- March 2016
-
- Article
- Export citation
Arithmetic of positive characteristic
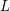 $L$-series values in Tate algebras
$L$-series values in Tate algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 1-61
- Print publication:
- January 2016
-
- Article
- Export citation
Cusp forms on the exceptional group of type
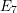 $E_{7}$
$E_{7}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 223-254
- Print publication:
- February 2016
-
- Article
- Export citation
A quasi-linear time algorithm for computing modular polynomials in dimension 2
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 603-632
-
- Article
-
- You have access
- Export citation
PARAMETRIZING ELLIPTIC CURVES BY MODULAR UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 33-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE DOUBLE COVER OF ODD GENERAL SPIN GROUPS, SMALL REPRESENTATIONS, AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 07 August 2015, pp. 609-671
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
- Print publication:
- December 2015
-
- Article
- Export citation