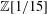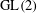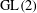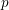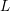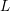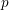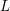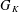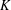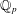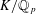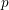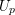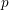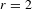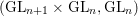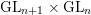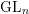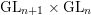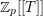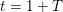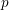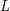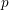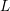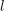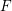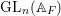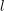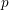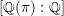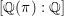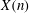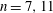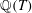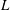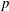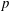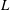Refine listing
Actions for selected content:
599 results in 11Fxx
THE SHIMURA CURVE OF DISCRIMINANT 15 AND TOPOLOGICAL AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 05 February 2015, e3
-
- Article
-
- You have access
- Open access
- Export citation
THE WEIGHT PART OF SERRE’S CONJECTURE FOR
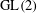 $\text{GL}(2)$
$\text{GL}(2)$
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 05 February 2015, e2
-
- Article
-
- You have access
- Open access
- Export citation
The
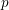 $p$-adic
$p$-adic 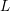 $L$-functions of evil Eisenstein series
$L$-functions of evil Eisenstein series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 13 January 2015, pp. 999-1040
- Print publication:
- June 2015
-
- Article
- Export citation
THE BREUIL–MÉZARD CONJECTURE FOR POTENTIALLY BARSOTTI–TATE REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 2 / 2014
- Published online by Cambridge University Press:
- 22 December 2014, e1
-
- Article
-
- You have access
- Open access
- Export citation
Level 1 Hecke algebras of modular forms modulo
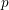 $p$
$p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
- Print publication:
- March 2015
-
- Article
- Export citation
On the anticyclotomic Iwasawa main conjecture for modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 863-897
- Print publication:
- May 2015
-
- Article
- Export citation
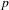 $p$-ADIC EISENSTEIN SERIES AND
$p$-ADIC EISENSTEIN SERIES AND  $L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
$L$-FUNCTIONS OF CERTAIN CUSP FORMS ON DEFINITE UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 21 November 2014, pp. 471-510
- Print publication:
- July 2016
-
- Article
- Export citation
Periods of automorphic forms: the case of
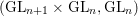 $(\text{GL}_{n+1}\times \text{GL}_{n},\text{GL}_{n})$
$(\text{GL}_{n+1}\times \text{GL}_{n},\text{GL}_{n})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 665-712
- Print publication:
- April 2015
-
- Article
- Export citation
Big Galois representations and
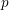 $p$-adic
$p$-adic 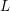 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 13 November 2014, pp. 603-664
- Print publication:
- April 2015
-
- Article
- Export citation
Automorphy and irreducibility of some l-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 207-229
- Print publication:
- February 2015
-
- Article
- Export citation
Galois representations attached to moments of Kloosterman sums and conjectures of Evans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 October 2014, pp. 68-120
- Print publication:
- January 2015
-
- Article
- Export citation
Unitary cycles on Shimura curves and the Shimura lift II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 15 September 2014, pp. 1963-2002
- Print publication:
- December 2014
-
- Article
- Export citation
On fields of rationality for automorphic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 11 September 2014, pp. 2003-2053
- Print publication:
- December 2014
-
- Article
- Export citation
On families of 7- and 11-congruent elliptic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 536-564
-
- Article
-
- You have access
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
On the computation of the determinant of vector-valued Siegel modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 247-256
-
- Article
-
- You have access
- Export citation
Computing Galois representations of modular abelian surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 36-48
-
- Article
-
- You have access
- Export citation
Nonvanishing of twists of
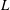 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L$-functions attached to Hilbert modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 330-348
-
- Article
-
- You have access
- Export citation
Modularity lifting results in parallel weight one and applications to the Artin conjecture: the tamely ramified case
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 July 2014, e18
-
- Article
-
- You have access
- Open access
- Export citation
RAMANUJAN SERIES UPSIDE-DOWN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 07 July 2014, pp. 78-106
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation