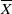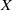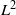Refine listing
Actions for selected content:
599 results in 11Fxx
Ternary quadratic forms and half-integral weight modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 418-435
-
- Article
-
- You have access
- Export citation
Differential equations and expansions for quaternionic modular forms in the discriminant 6 case
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 385-399
-
- Article
-
- You have access
- Export citation
p-adic modular forms of non-integral weight over Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 01 November 2012, pp. 32-62
- Print publication:
- January 2013
-
- Article
- Export citation
Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1655-1694
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Schwarzian differential equations and Hecke eigenforms on Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1-31
- Print publication:
- January 2013
-
- Article
- Export citation
On arithmetic families of filtered
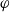 $\varphi $-modules and crystalline representations
$\varphi $-modules and crystalline representations
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 19 September 2012, pp. 677-726
- Print publication:
- October 2013
-
- Article
- Export citation
Boundary behaviour of special cohomology classes arising from the Weil representation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 03 July 2012, pp. 571-634
- Print publication:
- July 2013
-
- Article
- Export citation
On Greenberg’s L-invariant of the symmetric sixth power of an ordinary cusp form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1033-1050
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
CM cycles on Shimura curves, and p-adic L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 4 / July 2012
- Published online by Cambridge University Press:
- 15 May 2012, pp. 1003-1032
- Print publication:
- July 2012
-
- Article
-
- You have access
- Export citation
Slopes of the U7 operator acting on a space of overconvergent modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 113-139
-
- Article
-
- You have access
- Export citation
On the automorphy of l-adic Galois representations with small residual image With an appendix by Robert Guralnick, Florian Herzig, Richard Taylor and Jack Thorne
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 05 April 2012, pp. 855-920
- Print publication:
- October 2012
-
- Article
- Export citation
The L2 restriction norm of a GL3 Maass form
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 20 March 2012, pp. 675-717
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Quantifying residual finiteness of arithmetic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 907-920
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Local spectral equidistribution for Siegel modular forms and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 21 February 2012, pp. 335-384
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Opérateur de Lefschetz sur les tours de Drinfeld et Lubin–Tate
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 25 January 2012, pp. 507-530
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A non-solvable extension of ℚ unramified outside 7
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 24 January 2012, pp. 669-674
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
From L-series of elliptic curves to Mahler measures
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 23 January 2012, pp. 385-414
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Generalized affine Springer fibres
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 03 January 2012, pp. 569-609
- Print publication:
- July 2012
-
- Article
- Export citation
Locally analytic vectors of some crystabelian representations of GL2(ℚp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 20 December 2011, pp. 28-64
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
QUASIMODULAR FORMS AND COHOMOLOGY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 15 December 2011, pp. 150-163
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation