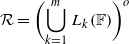Refine listing
Actions for selected content:
599 results in 11Fxx
A twisted topological trace formula for Hecke operators and liftings from symplectic to general linear groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 65-120
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
On the AF-algebra of a Hecke eigenform
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 207-213
-
- Article
-
- You have access
- Export citation
Algebraic integers as special values of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 167-179
-
- Article
-
- You have access
- Export citation
The sign of Galois representations attached to automorphic forms for unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 27 July 2011, pp. 1337-1352
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
On anticyclotomic μ-invariants of modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 27 July 2011, pp. 1353-1381
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
On the Siegel–Weil formula: The case of singular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 04 May 2011, pp. 1003-1021
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
On the continuity of Arthur’s trace formula: the semisimple terms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 06 April 2011, pp. 784-802
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Vanishing of the μ-invariant of p-adic Hecke L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 24 March 2011, pp. 1151-1178
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Modularity lifting theorems for Galois representations of unitary type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 18 March 2011, pp. 1022-1058
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Nonsolvable number fields ramified only at 3 and 5
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 716-734
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Dichotomy for generic supercuspidal representations of G2
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 15 February 2011, pp. 735-783
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Serre weights for quaternion algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 09 February 2011, pp. 1059-1086
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
A strengthening of the GL(2) converse theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 669-715
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
Iwasawa theory for modular forms at supersingular primes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 803-838
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
A NOTE ON FOURIER COEFFICIENTS OF POINCARÉ SERIES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 31-40
- Print publication:
- January 2011
-
- Article
- Export citation
EFFICIENTLY GENERATED SPACES OF CLASSICAL SIEGEL MODULAR FORMS AND THE BÖCHERER CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 01 April 2011, pp. 393-405
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON FOURIER COEFFICIENTS OF MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 26 November 2010, pp. 50-62
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
NONVANISHING OF JACOBI POINCARÉ SERIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 12 January 2011, pp. 165-179
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
CONVEX STANDARD FUNDAMENTAL DOMAIN FOR SUBGROUPS OF HECKE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 14 September 2010, pp. 96-107
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
One level density of low-lying zeros of families of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 1-18
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
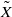 by gluing together 2
by gluing together 2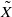 and get formulas for the traces of Hecke operators ℋ acting on the cohomology of
and get formulas for the traces of Hecke operators ℋ acting on the cohomology of 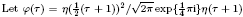 , where
, where 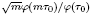 is an algebraic integer dividing
is an algebraic integer dividing 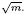 This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when
This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when 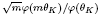 is a unit.
is a unit.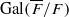 which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre
which is modular in the sense that it comes from an automorphic form on a definite quaternion algebra with centre