Refine listing
Actions for selected content:
599 results in 11Fxx
NEW REPRESENTATIONS FOR APÉRY-LIKE SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 10 December 2009, pp. 107-117
- Print publication:
- January 2010
-
- Article
- Export citation
Regular and residual Eisenstein series and the automorphic cohomology of Sp(2,2)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 November 2009, pp. 21-57
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On Ihara’s lemma for Hilbert modular varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 09 September 2009, pp. 1114-1146
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Hilbert modular forms and p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 5 / September 2009
- Published online by Cambridge University Press:
- 21 September 2009, pp. 1081-1113
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Subconvexity bounds for automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 95-124
- Print publication:
- January 2010
-
- Article
- Export citation
LIFTING PUZZLES IN DEGREE FOUR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 06 July 2009, pp. 65-82
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
QUASIMODULAR FORMS AND VECTOR BUNDLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 402-412
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Level-raising for Saito–Kurokawa forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 915-953
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Classification of two-dimensional split trianguline representations of p-adic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 865-914
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
Poles of L-functions and theta liftings for orthogonal groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 10 June 2009, pp. 693-741
- Print publication:
- October 2009
-
- Article
- Export citation
On the Eisenstein ideal for imaginary quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 603-632
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
q-series and weight 3/2 Maass forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 541-552
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Mock Jacobi forms in basic hypergeometric series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 553-565
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
A Plancherel formula for Sp2n/Spn×Spn and its application
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 501-527
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Intersection theory on Shimura surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 423-475
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
A deformation problem for Galois representations over imaginary quadratic fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 669-692
- Print publication:
- October 2009
-
- Article
- Export citation
Potential level-lowering for GSp(4)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 595-622
- Print publication:
- July 2009
-
- Article
- Export citation
Presque Cp-représentations et (ϕ,Γ)-modules
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 653-668
- Print publication:
- October 2009
-
- Article
- Export citation
Analytic vectors in continuous p-adic representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 247-270
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
The exceptional zero conjecture for Hilbert modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 01 January 2009, pp. 1-55
- Print publication:
- January 2009
-
- Article
-
- You have access
- Export citation
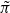 congruent to
congruent to 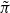 back to GSp(4), we use Arthur’s stable trace formula. Since
back to GSp(4), we use Arthur’s stable trace formula. Since 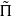 of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for
of GSp(4), congruent to Π, which is neither CAP nor endoscopic. It is crucial for our application that we can arrange for 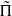 to have vectors fixed by the non-special maximal compact subgroups at all primes dividing
to have vectors fixed by the non-special maximal compact subgroups at all primes dividing 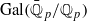 for
for 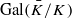 using
using 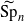 .
.