Refine listing
Actions for selected content:
599 results in 11Fxx
Transfert d’intégrales orbitales pour le groupe métaplectique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 524-590
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On endoscopy and the refined Gross–Prasad conjecture for (SO5, SO4)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 235-324
- Print publication:
- April 2011
-
- Article
- Export citation
Geometric level raising for p-adic automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 05 August 2010, pp. 335-354
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
THE ACTION OF HECKE OPERATORS ON HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 21 September 2010, pp. 51-74
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Fundamental domains for genus-zero and genus-one congruence subgroups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 July 2010, pp. 222-245
-
- Article
-
- You have access
- Export citation
ON A CLASS OF GENERALIZED FERMAT EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 June 2010, pp. 505-510
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
K1 of products of Drinfeld modular curves and special values of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 886-918
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Unitary dual of GL(n) at archimedean places and global Jacquet–Langlands correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 5 / September 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 1115-1164
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Le lemme fondamental pondéré. I. Constructions géométriques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 6 / November 2010
- Published online by Cambridge University Press:
- 19 May 2010, pp. 1416-1506
- Print publication:
- November 2010
-
- Article
-
- You have access
- Export citation
On mean values and non-vanishing of derivatives of L-functions in a nonlinear family
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 April 2010, pp. 19-34
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Automorphisms of hyperelliptic modular curves X0(N) in positive characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 April 2010, pp. 144-163
-
- Article
-
- You have access
- Export citation
The semisimplicity conjecture for A-motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 561-598
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
On the potential automorphy of certain odd-dimensional Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 10 March 2010, pp. 607-620
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Analytic continuation of overconvergent Hilbert eigenforms in the totally split case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 02 February 2010, pp. 541-560
- Print publication:
- May 2010
-
- Article
-
- You have access
- Export citation
Special Values of Class Group L-Functions for CM Fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-181
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
HEAT OPERATORS AND QUASIMODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 28 January 2010, pp. 514-522
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
RANKIN’S METHOD AND JACOBI FORMS OF SEVERAL VARIABLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 131-143
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
Moduli spaces of irreducible symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 404-434
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Spectral decomposition of compactly supported Poincaré series and existence of cusp forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 1-20
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
On some modular representations of the Borel subgroup of GL2(Qp)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 December 2009, pp. 58-80
- Print publication:
- January 2010
-
- Article
-
- You have access
- Export citation
 of a modular curve
of a modular curve 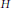
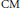
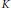


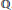
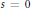

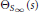
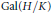
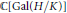
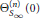
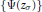
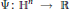
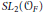
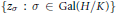
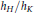
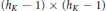
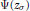
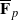 -representation
-representation 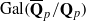 by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(
by using Fontaine’s theory of (φ,Γ)-modules. We compute Ω(