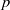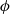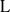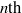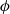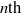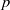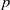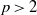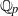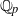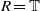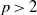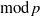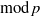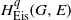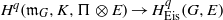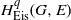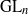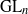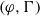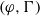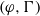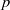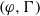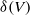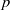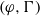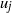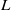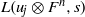Refine listing
Actions for selected content:
599 results in 11Fxx
ON THE INTEGRAL HODGE AND TATE CONJECTURES OVER A NUMBER FIELD
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 12 September 2013, e4
-
- Article
-
- You have access
- Open access
- Export citation
On the Kohnen plus space for Hilbert modular forms of half-integral weight I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 12 / December 2013
- Published online by Cambridge University Press:
- 06 September 2013, pp. 1963-2010
- Print publication:
- December 2013
-
- Article
- Export citation
Higher torsion in the Abelianization of the full Bianchi groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 September 2013, pp. 344-365
-
- Article
-
- You have access
- Export citation
Computing Borcherds products
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 200-215
-
- Article
-
- You have access
- Export citation
On level one cuspidal Bianchi modular forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 187-199
-
- Article
-
- You have access
- Export citation
Explicit application of Waldspurger’s theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 216-245
-
- Article
-
- You have access
- Export citation
Computing level one Hecke eigensystems (mod
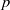 $p$ )
$p$ )
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
A geometric perspective on the Breuil–Mézard conjecture
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 26 June 2013, pp. 183-223
- Print publication:
- January 2014
-
- Article
- Export citation
Companion forms in parallel weight one
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 10 May 2013, pp. 903-913
- Print publication:
- June 2013
-
- Article
- Export citation
Residues of Eisenstein series and the automorphic cohomology of reductive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 07 May 2013, pp. 1061-1090
- Print publication:
- July 2013
-
- Article
- Export citation
A local-global question in automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 April 2013, pp. 959-995
- Print publication:
- June 2013
-
- Article
- Export citation
A GENERATING FUNCTION OF THE SQUARES OF LEGENDRE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 22 March 2013, pp. 125-131
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Cusp eigenforms and the hall algebra of an elliptic curve
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 04 March 2013, pp. 914-958
- Print publication:
- June 2013
-
- Article
- Export citation
Iwasawa theory of de Rham
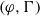 $(\varphi , \Gamma )$-modules over the Robba ring
$(\varphi , \Gamma )$-modules over the Robba ring
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 27 February 2013, pp. 65-118
- Print publication:
- January 2014
-
- Article
- Export citation
On admissible tensor products in p-adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 14 February 2013, pp. 417-429
- Print publication:
- March 2013
-
- Article
- Export citation
DISSOLVING OF CUSP FORMS: HIGHER-ORDER FERMI’S GOLDEN RULES
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 21 January 2013, pp. 269-301
- Print publication:
- July 2013
-
- Article
- Export citation
Hybrid bounds for automorphic forms on ellipsoids over number fields
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 727-758
- Print publication:
- October 2013
-
- Article
- Export citation
On the gcd of local Rankin–Selberg integrals for even orthogonal groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 587-636
- Print publication:
- April 2013
-
- Article
- Export citation
Dihedral Iwasawa theory of nearly ordinary quaternionic automorphic forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 13 December 2012, pp. 356-416
- Print publication:
- March 2013
-
- Article
- Export citation