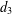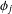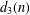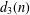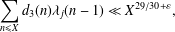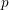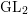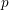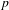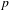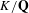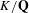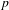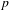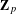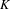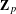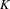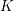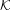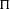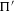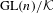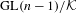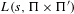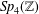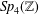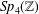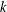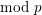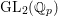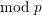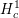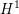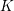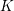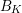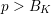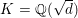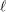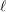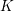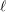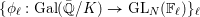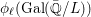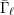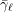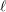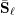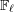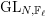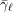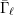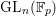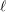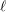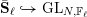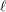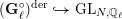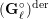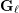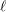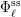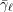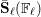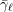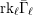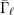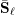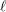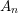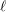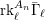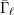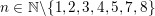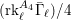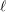Refine listing
Actions for selected content:
599 results in 11Fxx
FACTORIALS AND THE RAMANUJAN FUNCTION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 177-185
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
EXCEPTIONAL ZEROES OF P-ADIC L-FUNCTIONS OVER NON-ABELIAN FIELD EXTENSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 385-432
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
AVERAGES OF TWISTED
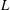 $L$-FUNCTIONS
$L$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 24 June 2015, pp. 207-236
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
SPECIAL VALUES OF SHIFTED CONVOLUTION DIRICHLET SERIES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 16 June 2015, pp. 47-66
- Print publication:
- 2016
-
- Article
- Export citation
THE MOONSHINE MODULE FOR CONWAY’S GROUP
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 15 June 2015, e10
-
- Article
-
- You have access
- Open access
- Export citation
Some applications of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 03 June 2015, pp. 91-106
-
- Article
- Export citation
SHIFTED CONVOLUTION SUM OF
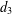 $d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS
$d_{3}$ AND THE FOURIER COEFFICIENT OF HECKE–MAASS FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 195-204
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Beyond endoscopy via the trace formula: 1. Poisson summation and isolation of special representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1791-1820
- Print publication:
- October 2015
-
- Article
- Export citation
On the smooth transfer for Guo–Jacquet relative trace formulae
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 10 / October 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1821-1877
- Print publication:
- October 2015
-
- Article
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation
ON THE NON-TRIVIALITY OF THE
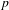 $p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO
$p$ -ADIC ABEL–JACOBI IMAGE OF GENERALISED HEEGNER CYCLES MODULO 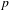 $p$ , II: SHIMURA CURVES
$p$ , II: SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 07 May 2015, pp. 189-222
- Print publication:
- February 2017
-
- Article
- Export citation
IMPROPER INTERSECTIONS OF KUDLA–RAPOPORT DIVISORS AND EISENSTEIN SERIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 23 April 2015, pp. 899-945
- Print publication:
- November 2017
-
- Article
- Export citation
Euler systems for modular forms over imaginary quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 9 / September 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1585-1625
- Print publication:
- September 2015
-
- Article
- Export citation
Computing overconvergent forms for small primes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 250-257
-
- Article
-
- You have access
- Export citation
WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT
 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 31 March 2015, pp. 711-769
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SOME MONODROMY GROUPS OF FINITE INDEX IN
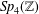 $\mathit{Sp}_{4}(\mathbb{Z})$
$\mathit{Sp}_{4}(\mathbb{Z})$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 30 March 2015, pp. 48-62
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON POWER MOMENTS OF THE HECKE MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 25 March 2015, pp. 334-340
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
On
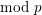 $\text{mod}~p$ non-abelian Lubin–Tate theory for
$\text{mod}~p$ non-abelian Lubin–Tate theory for 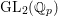 $\text{GL}_{2}(\mathbb{Q}_{p})$
$\text{GL}_{2}(\mathbb{Q}_{p})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 12 March 2015, pp. 1433-1461
- Print publication:
- August 2015
-
- Article
- Export citation
The asymptotic Fermat’s Last Theorem for five-sixths of real quadratic fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 1395-1415
- Print publication:
- August 2015
-
- Article
- Export citation
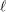 $\ell$-independence for compatible systems of (mod
$\ell$-independence for compatible systems of (mod 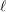 $\ell$) representations
$\ell$) representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 02 March 2015, pp. 1215-1241
- Print publication:
- July 2015
-
- Article
- Export citation
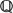
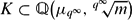
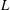
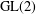
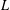
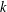
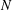
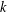
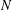
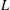
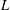
 .
.