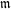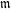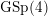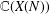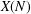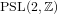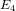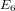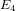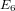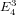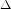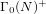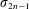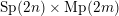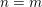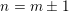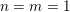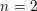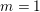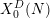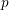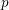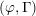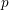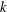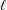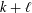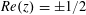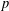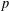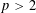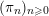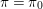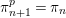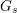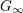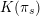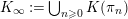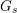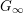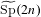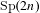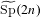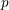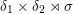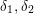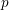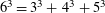Refine listing
Actions for selected content:
599 results in 11Fxx
On the fourth moment of Hecke–Maass forms and the random wave conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 7 / July 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1479-1511
- Print publication:
- July 2017
-
- Article
- Export citation
BEYOND ENDOSCOPY FOR THE RELATIVE TRACE FORMULA II: GLOBAL THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 24 April 2017, pp. 347-447
- Print publication:
- March 2019
-
- Article
- Export citation
SUR LA TORSION DANS LA COHOMOLOGIE DES VARIÉTÉS DE SHIMURA DE KOTTWITZ-HARRIS-TAYLOR
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 30 March 2017, pp. 499-517
- Print publication:
- May 2019
-
- Article
- Export citation
On higher regulators of Siegel threefolds II: the connection to the special value
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 889-946
- Print publication:
- May 2017
-
- Article
- Export citation
Bezout-type theorems for differential fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 867-888
- Print publication:
- April 2017
-
- Article
- Export citation
NORMAL BASES FOR MODULAR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 384-392
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON THE TENTH-ORDER MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 March 2017, pp. 44-62
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Certain aspects of holomorphic function theory on some genus-zero arithmetic groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 360-381
-
- Article
-
- You have access
- Export citation
ZETA ELEMENTS IN DEPTH 3 AND THE FUNDAMENTAL LIE ALGEBRA OF THE INFINITESIMAL TATE CURVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 05 January 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation
Refined global Gan–Gross–Prasad conjecture for Fourier–Jacobi periods on symplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 68-131
- Print publication:
- January 2017
-
- Article
- Export citation
Equations of hyperelliptic Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 1-40
- Print publication:
- January 2017
-
- Article
- Export citation
Paraboline variation over
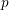 $p$ -adic families of
$p$ -adic families of 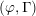 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 19 January 2017, pp. 132-174
- Print publication:
- January 2017
-
- Article
- Export citation
ZEROS OF CERTAIN COMBINATIONS OF EISENSTEIN SERIES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 10 August 2017, pp. 666-695
- Print publication:
- 2017
-
- Article
- Export citation
SERRE WEIGHTS AND WILD RAMIFICATION IN TWO-DIMENSIONAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 23 December 2016, e33
-
- Article
-
- You have access
- Open access
- Export citation
ON GALOIS EQUIVARIANCE OF HOMOMORPHISMS BETWEEN TORSION CRYSTALLINE REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 13 December 2016, pp. 169-214
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
SPECTRAL TRANSFER FOR METAPLECTIC GROUPS. I. LOCAL CHARACTER RELATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 07 December 2016, pp. 25-123
- Print publication:
- January 2019
-
- Article
- Export citation
WEIGHT CHANGING OPERATORS FOR AUTOMORPHIC FORMS ON GRASSMANNIANS AND DIFFERENTIAL PROPERTIES OF CERTAIN THETA LIFTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 28 November 2016, pp. 186-221
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON THE FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 234 / June 2019
- Published online by Cambridge University Press:
- 21 October 2016, pp. 1-16
- Print publication:
- June 2019
-
- Article
-
- You have access
- HTML
- Export citation
COMPOSITION FACTORS OF A CLASS OF INDUCED REPRESENTATIONS OF CLASSICAL
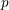 $p$ -ADIC GROUPS
$p$ -ADIC GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 16-48
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
PERFECT POWERS THAT ARE SUMS OF CONSECUTIVE CUBES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 230-249
- Print publication:
- 2017
-
- Article
- Export citation