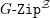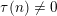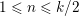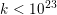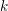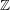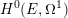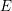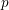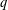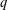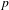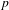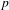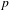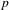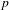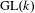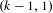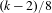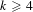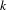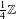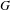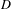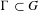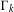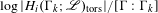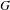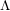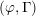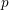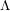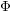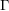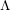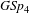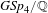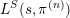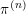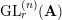Refine listing
Actions for selected content:
599 results in 11Fxx
Automorphic vector bundles with global sections on
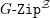 $G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
$G\text{-}\mathtt{Zip}^{{\mathcal{Z}}}$-schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 31 October 2018, pp. 2586-2605
- Print publication:
- December 2018
-
- Article
- Export citation
RAMANUJAN SERIES WITH A SHIFT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 23 October 2018, pp. 367-380
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Random ordering in modulus of consecutive Hecke eigenvalues of primitive forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 18 October 2018, pp. 2441-2461
- Print publication:
- November 2018
-
- Article
- Export citation
COMPACTIFICATIONS OF SUBSCHEMES OF INTEGRAL MODELS OF SHIMURA VARIETIES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 24 September 2018, e18
-
- Article
-
- You have access
- Open access
- Export citation
LINEAR INDEPENDENCE OF POWERS OF SINGULAR MODULI OF DEGREE THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 12 September 2018, pp. 42-50
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
On two arithmetic theta lifts
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 10 / October 2018
- Published online by Cambridge University Press:
- 07 September 2018, pp. 2090-2149
- Print publication:
- October 2018
-
- Article
- Export citation
KERNEL FUNCTIONS OF THE TWISTED SYMMETRIC SQUARE OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 1 / 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 130-131
- Print publication:
- 2019
-
- Article
-
- You have access
- HTML
- Export citation
The Manin constant in the semistable case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 13 August 2018, pp. 1889-1920
- Print publication:
- September 2018
-
- Article
- Export citation
Siegel families with application to class fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 27 June 2018, pp. 751-771
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
LIFTING N-DIMENSIONAL GALOIS REPRESENTATIONS TO CHARACTERISTIC ZERO
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 115-150
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
THETA BLOCK FOURIER EXPANSIONS, BORCHERDS PRODUCTS AND A SEQUENCE OF NEWMAN AND SHANKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 14 June 2018, pp. 48-59
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
RANKIN–SELBERG CONVOLUTIONS OF NONCUSPIDAL HALF-INTEGRAL WEIGHT MAASS FORMS IN THE PLUS SPACE
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 21 May 2018, pp. 127-165
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ATTACHED TO HILBERT MODULAR FORMS MOD
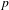 $p$ OF WEIGHT 1
$p$ OF WEIGHT 1
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 23 April 2018, pp. 281-306
- Print publication:
- March 2020
-
- Article
- Export citation
A p-ADIC HERMITIAN MAASS LIFT
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 17 April 2018, pp. 85-114
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF ARITHMETIC GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 March 2018, pp. 537-569
- Print publication:
- March 2020
-
- Article
- Export citation
Pair correlation for quadratic polynomials mod 1
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 960-983
- Print publication:
- May 2018
-
- Article
- Export citation
The geometry of Hida families II:
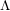 $\unicode[STIX]{x1D6EC}$ -adic
$\unicode[STIX]{x1D6EC}$ -adic 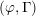 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$ -modules and 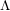 $\unicode[STIX]{x1D6EC}$ -adic Hodge theory
$\unicode[STIX]{x1D6EC}$ -adic Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 08 March 2018, pp. 719-760
- Print publication:
- April 2018
-
- Article
- Export citation
AN EQUIDISTRIBUTION THEOREM FOR HOLOMORPHIC SIEGEL MODULAR FORMS FOR
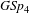 $\mathit{GSp}_{4}$ AND ITS APPLICATIONS
$\mathit{GSp}_{4}$ AND ITS APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 22 February 2018, pp. 351-419
- Print publication:
- March 2020
-
- Article
- Export citation
Generating functions on covering groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 671-684
- Print publication:
- April 2018
-
- Article
- Export citation