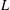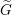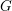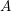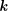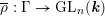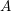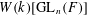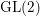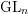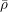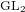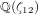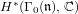Refine listing
Actions for selected content:
599 results in 11Fxx
Modular embeddings of Teichmüller curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 21 September 2016, pp. 2269-2349
- Print publication:
- November 2016
-
- Article
- Export citation
PARTIAL INDEFINITE THETA IDENTITIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 255-289
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Computing Jacobi forms
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 205-219
-
- Article
-
- You have access
- Export citation
IMAGES OF ADELIC GALOIS REPRESENTATIONS FOR MODULAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 03 August 2016, pp. 11-25
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
TORSION GALOIS REPRESENTATIONS OVER CM FIELDS AND HECKE ALGEBRAS IN THE DERIVED CATEGORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 21 July 2016, e21
-
- Article
-
- You have access
- Open access
- Export citation
ANDRÉ–OORT CONJECTURE AND NONVANISHING OF CENTRAL
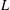 $L$ -VALUES OVER HILBERT CLASS FIELDS
$L$ -VALUES OVER HILBERT CLASS FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 20 July 2016, e20
-
- Article
-
- You have access
- Open access
- Export citation
On a lifting problem of L-packets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1800-1850
- Print publication:
- September 2016
-
- Article
- Export citation
The inverse deformation problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1725-1739
- Print publication:
- August 2016
-
- Article
- Export citation
Rational points on Erdős–Selfridge superelliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 11 / November 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 2249-2254
- Print publication:
- November 2016
-
- Article
- Export citation
A TRACE FORMULA FOR HECKE OPERATORS ON VECTOR-VALUED MODULAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 143-165
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
MOCK THETA DOUBLE SUMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 323-348
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
THE BERNSTEIN CENTER OF THE CATEGORY OF SMOOTH
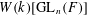 $W(k)[\text{GL}_{n}(F)]$ -MODULES
$W(k)[\text{GL}_{n}(F)]$ -MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 07 June 2016, e11
-
- Article
-
- You have access
- Open access
- Export citation
LIFTING TO GL(2) OVER A DIVISION QUATERNION ALGEBRA, AND AN EXPLICIT CONSTRUCTION OF CAP REPRESENTATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 222 / Issue 1 / June 2016
- Published online by Cambridge University Press:
- 07 June 2016, pp. 137-185
- Print publication:
- June 2016
-
- Article
-
- You have access
- HTML
- Export citation
Level raising mod 2 and arbitrary 2-Selmer ranks
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 01 June 2016, pp. 1576-1608
- Print publication:
- August 2016
-
- Article
- Export citation
On the image of complex conjugation in certain Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 1476-1488
- Print publication:
- July 2016
-
- Article
- Export citation
Density of potentially crystalline representations of fixed weight
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 1609-1647
- Print publication:
- August 2016
-
- Article
- Export citation
On some Fricke families and application to the Lang–Schertz conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 18 May 2016, pp. 723-740
- Print publication:
- August 2016
-
- Article
- Export citation
Modular elliptic curves over the field of twelfth roots of unity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 April 2016, pp. 155-174
-
- Article
-
- You have access
- Export citation
 $L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
$L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 22 March 2016, pp. 425-440
- Print publication:
- April 2018
-
- Article
- Export citation
Some applications of eta-quotients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 565-578
- Print publication:
- June 2016
-
- Article
- Export citation