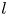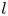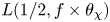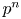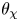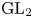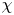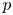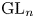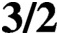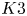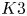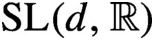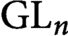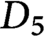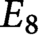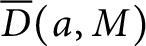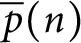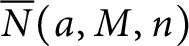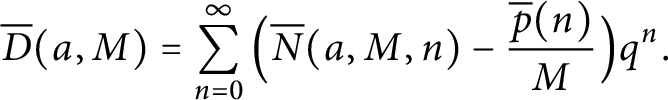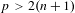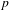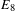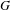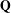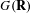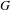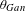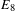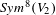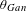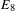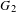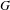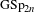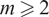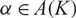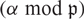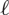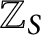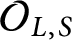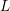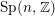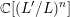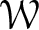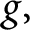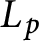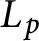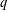Refine listing
Actions for selected content:
599 results in 11Fxx
Vanishing theorems for the mod p cohomology of some simple Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 November 2020, e38
-
- Article
-
- You have access
- Open access
- Export citation
Automorphy lifting for residually reducible
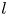 $l$-adic Galois representations, II
$l$-adic Galois representations, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2399-2422
- Print publication:
- November 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
Branching laws for classical groups: the non-tempered case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2298-2367
- Print publication:
- November 2020
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
CONGRUENCES MODULO 4 FOR WEIGHT
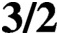 $\textbf{3/2}$ ETA-PRODUCTS
$\textbf{3/2}$ ETA-PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 405-417
- Print publication:
- June 2021
-
- Article
- Export citation
K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 19 November 2020, pp. 1965-2019
- Print publication:
- October 2020
-
- Article
- Export citation
CONGRUENCE PRIMES FOR SIEGEL MODULAR FORMS OF PARAMODULAR LEVEL AND APPLICATIONS TO THE BLOCH–KATO CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 September 2020, pp. 660-681
- Print publication:
- September 2021
-
- Article
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 September 2020, pp. 122-169
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
Dyson’s rank, overpartitions, and universal mock theta functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 687-696
- Print publication:
- September 2021
-
- Article
- Export citation
GLOBALLY REALIZABLE COMPONENTS OF LOCAL DEFORMATION RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 03 September 2020, pp. 533-602
- Print publication:
- March 2022
-
- Article
- Export citation
Arithmetic diagonal cycles on unitary Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1745-1824
- Print publication:
- September 2020
-
- Article
- Export citation
THE MINIMAL MODULAR FORM ON QUATERNIONIC
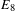 $E_{8}$
$E_{8}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 603-636
- Print publication:
- March 2022
-
- Article
- Export citation
Local intertwining relation for metaplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1560-1594
- Print publication:
- August 2020
-
- Article
- Export citation
REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS, II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 28 July 2020, pp. 484-502
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- Export citation
Finite descent obstruction for Hilbert modular varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 22 July 2020, pp. 452-473
- Print publication:
- June 2021
-
- Article
- Export citation
ANALYTIC PROPERTIES OF EISENSTEIN SERIES AND STANDARD
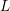 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 168-203
- Print publication:
- December 2021
-
- Article
- Export citation
Bounding Selmer Groups for the Rankin–Selberg Convolution of Coleman Families
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 805-853
- Print publication:
- June 2021
-
- Article
- Export citation
A
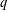 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 303-310
- Print publication:
- April 2021
-
- Article
- Export citation