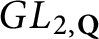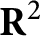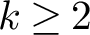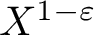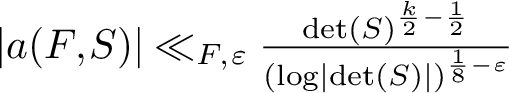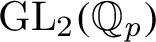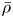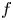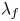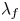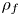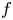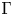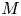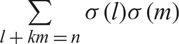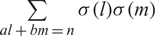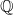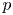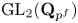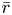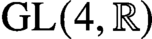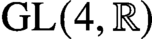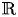Refine listing
Actions for selected content:
599 results in 11Fxx
Special curves in modular surfaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 December 2021, pp. 1-18
- Print publication:
- March 2023
-
- Article
- Export citation
TWISTED DOUBLING INTEGRALS FOR BRYLINSKI–DELIGNE EXTENSIONS OF CLASSICAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 01 December 2021, pp. 1931-1985
- Print publication:
- July 2023
-
- Article
- Export citation
GEOMETRIC WEIGHT-SHIFTING OPERATORS ON HILBERT MODULAR FORMS IN CHARACTERISTIC p
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 15 November 2021, pp. 1871-1930
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FUNDAMENTAL FOURIER COEFFICIENTS OF SIEGEL CUSP FORMS OF DEGREE 2
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 12 November 2021, pp. 1819-1869
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
AUTOMORPHIC LEFSCHETZ PROPERTIES FOR NONCOMPACT ARITHMETIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 1655-1702
- Print publication:
- July 2023
-
- Article
- Export citation
CONGRUENCES OF SAITO–KUROKAWA LIFTS AND DENOMINATORS OF CENTRAL SPINOR L-VALUES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 14 October 2021, pp. 504-525
- Print publication:
- May 2022
-
- Article
- Export citation
ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1067-1106
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
An arithmetic property of intertwining operators for p-adic groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 September 2021, pp. 83-107
- Print publication:
- February 2023
-
- Article
- Export citation
ON THE MODULARITY OF SOLUTIONS TO CERTAIN DIFFERENTIAL EQUATIONS OF HYPERGEOMETRIC TYPE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 15 September 2021, pp. 385-391
- Print publication:
- June 2022
-
- Article
- Export citation
Wiles defect for Hecke algebras that are not complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 16 August 2021, pp. 2046-2088
- Print publication:
- September 2021
-
- Article
- Export citation
The classification of free algebras of orthogonal modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 06 August 2021, pp. 2026-2045
- Print publication:
- September 2021
-
- Article
- Export citation
ON NONCRITICAL GALOIS REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 July 2021, pp. 383-420
- Print publication:
- January 2023
-
- Article
- Export citation
EVALUATION OF CONVOLUTION SUMS
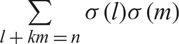 $$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 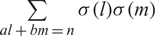 $$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 434-453
- Print publication:
- May 2022
-
- Article
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
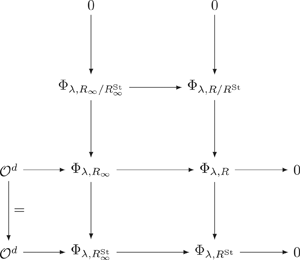
Diagrams in the mod p cohomology of Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 07 July 2021, pp. 1653-1723
- Print publication:
- August 2021
-
- Article
- Export citation
An orthogonality relation for
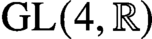 $\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)
$\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e47
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum: On the cuspidal cohomology of S-arithmetic subgroups of reductive groups over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 26 May 2021, pp. 1207-1210
- Print publication:
- June 2021
-
- Article
-
- You have access
- HTML
- Export citation
Prime geodesics and averages of the Zagier L-series
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 705-728
- Print publication:
- May 2022
-
- Article
- Export citation
Singular units and isogenies between CM elliptic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 1022-1035
- Print publication:
- May 2021
-
- Article
- Export citation