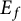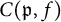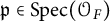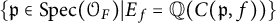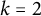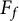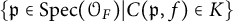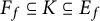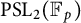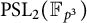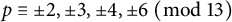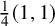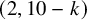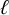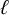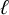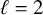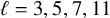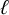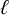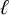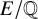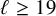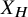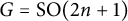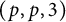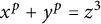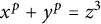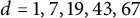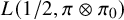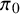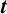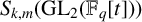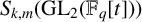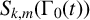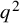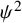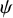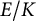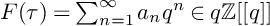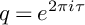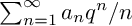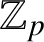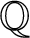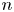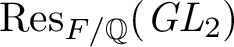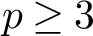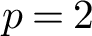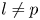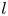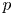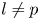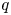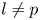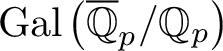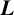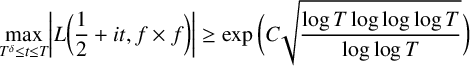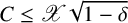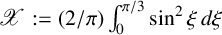Refine listing
Actions for selected content:
599 results in 11Fxx
On generation of the coefficient field of a primitive Hilbert modular form by a single Fourier coefficient
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 08 September 2022, pp. 587-598
- Print publication:
- June 2023
-
- Article
- Export citation
Modular forms and some cases of the Inverse Galois Problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 568-586
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic torsion for log-Enriques surfaces and Borcherds product
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shintani lifts of nearly holomorphic modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 19 August 2022, pp. 1446-1492
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
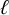 $\ell $-adic images of Galois for elliptic curves over
$\ell $-adic images of Galois for elliptic curves over  $\mathbb {Q}$ (and an appendix with John Voight)
$\mathbb {Q}$ (and an appendix with John Voight)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 August 2022, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ternary Diophantine equations of signature
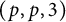 $(p,p,\text{3})$ over number fields
$(p,p,\text{3})$ over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1293-1313
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The second moment of
 $\mathrm {GL}(n)\times \mathrm {GL}(n)$ Rankin–Selberg L-functions
$\mathrm {GL}(n)\times \mathrm {GL}(n)$ Rankin–Selberg L-functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 June 2022, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HECKE OPERATORS AND DRINFELD CUSP FORMS OF LEVEL
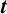 $\boldsymbol {t}$
$\boldsymbol {t}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 184-195
- Print publication:
- April 2023
-
- Article
- Export citation
Some cases of Kudla’s modularity conjecture for unitary Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motohashi’s formula for the fourth moment of individual Dirichlet L-functions and applications
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On elliptic curves with p-isogenies over quadratic fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 07 June 2022, pp. 945-964
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric orbital integrals and the center of the enveloping algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1189-1253
- Print publication:
- June 2022
-
- Article
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FINE SELMER GROUPS AND SIGNED SELMER GROUPS OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 419-430
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the algebraicity about the Hodge numbers of the Hilbert schemes of algebraic surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 392-403
-
- Article
- Export citation
ON A PROPERNESS OF THE HILBERT EIGENVARIETY AT INTEGRAL WEIGHTS: THE CASE OF QUADRATIC RESIDUE FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 08 April 2022, pp. 2645-2716
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic local deformation rings when
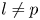 $l \neq p$
$l \neq p$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 721-749
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REDUCTIONS OF
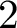 $2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE
$2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE 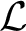 $\mathcal L$-INVARIANT
$\mathcal L$-INVARIANT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 01 April 2022, pp. 2619-2644
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTREME VALUES OF THE RANKIN–SELBERG
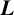 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 408-418
- Print publication:
- December 2022
-
- Article
- Export citation