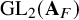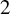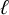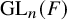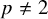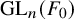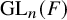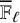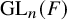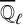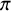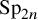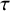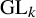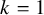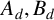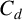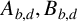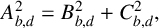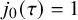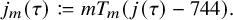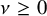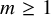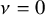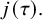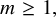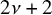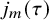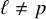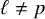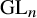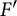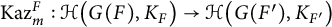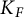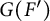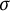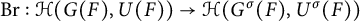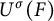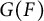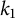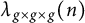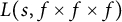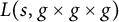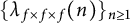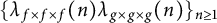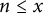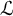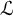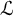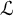Refine listing
Actions for selected content:
604 results in 11Fxx
Kodaira–Spencer isomorphisms and degeneracy maps on Iwahori-level Hilbert modular varieties: the saving trace
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 February 2025, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 325-355
- Print publication:
- September 2025
-
- Article
- Export citation
Asymptotics and sign patterns of Hecke polynomial coefficients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 914-926
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Ramanujan and Sato–Tate Conjectures for Bianchi modular forms
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 21 February 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cuspidal
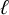 ${\ell }$-modular representations of
${\ell }$-modular representations of 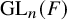 $\operatorname {GL}_n({ F})$ distinguished by a Galois involution
$\operatorname {GL}_n({ F})$ distinguished by a Galois involution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 February 2025, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local Galois deformation rings: generalised tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Doubling constructions and tensor product L-functions: coverings of the symplectic group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 10 February 2025, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANK 2
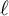 $\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
$\ell $-ADIC LOCAL SYSTEMS AND HIGGS BUNDLES OVER A CURVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 891-960
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ANALOGUE OF AN IDENTITY OF JACOBI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 528-535
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED RUELLE ZETA FUNCTION ON HYPERBOLIC MANIFOLDS AND COMPLEX-VALUED ANALYTIC TORSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 813-845
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L-series for Vector-Valued Weakly Holomorphic Modular Forms and Converse Theorems
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 January 2025, pp. 1-26
-
- Article
- Export citation
DERIVATIVES OF THETA FUNCTIONS AS TRACES OF PARTITION EISENSTEIN SERIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 284-295
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Control theorems for Hilbert modular varieties
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 530-549
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Eichler–Selberg relations for singular moduli
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theta functions, fourth moments of eigenforms, and the sup-norm problem I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2916-2969
- Print publication:
- December 2024
-
- Article
- Export citation
Lifting G-Valued Galois Representations when
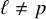 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compatibility of Kazhdan and Brauer homomorphism
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 19-43
- Print publication:
- March 2025
-
- Article
- Export citation
Results on the non-vanishing of derivatives of L-functions of vector-valued modular forms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 63-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the sign changes of Dirichlet coefficients of triple product L-functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1092-1106
- Print publication:
- December 2024
-
- Article
- Export citation
On Greenberg–Benois
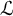 $\mathcal {L}$-invariants and Fontaine–Mazur
$\mathcal {L}$-invariants and Fontaine–Mazur 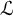 $\mathcal {L}$-invariants
$\mathcal {L}$-invariants
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1141-1160
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation