Max-stable random fields play a central role in modeling extreme value phenomena. We obtain an explicit formula for the conditional probability in general max-linear models, which include a large class of max-stable random fields. As a consequence, we develop an algorithm for efficient and exact sampling from the conditional distributions. Our method provides a computational solution to the prediction problem for spectrally discrete max-stable random fields. This work offers new tools and a new perspective to many statistical inference problems for spatial extremes, arising, for example, in meteorology, geology, and environmental applications.

We consider a feed-forward network with a single-server station serving jobs with multiple levels of priority. The service discipline is preemptive in that the server always serves a job with the current highest level of priority. For this system with discontinuous dynamics, we establish the sample path large deviation principle using a weak convergence argument. In the special case where jobs have two different levels of priority, we also explicitly identify the exponential decay rate of the total population overflow probabilities by examining the geometry of the zero-level sets of the system Hamiltonians.

We present a method for computing the probability density function (PDF) and the cumulative distribution function (CDF) of a nonnegative infinitely divisible random variable X. Our method uses the Lévy-Khintchine representation of the Laplace transform Ee-λX = e-ϕ(λ), where ϕ is the Laplace exponent. We apply the Post-Widder method for Laplace transform inversion combined with a sequence convergence accelerator to obtain accurate results. We demonstrate this technique on several examples, including the stable distribution, mixtures thereof, and integrals with respect to nonnegative Lévy processes.

In this paper we prove that the stationary distribution of populations in genetic algorithms focuses on the uniform population with the highest fitness value as the selective pressure goes to ∞ and the mutation probability goes to 0. The obtained sufficient condition is based on the work of Albuquerque and Mazza (2000), who, following Cerf (1998), applied the large deviation principle approach (Freidlin-Wentzell theory) to the Markov chain of genetic algorithms. The sufficient condition is more general than that of Albuquerque and Mazza, and covers a set of parameters which were not found by Cerf.

This paper demonstrates the application of a new higher-order weak approximation, called the Kusuoka approximation, with discrete random variables to non-commutative multi-factor models. Our experiments show that using the Heath–Jarrow–Morton model to price interest-rate derivatives can be practically feasible if the Kusuoka approximation is used along with the tree-based branching algorithm.

Geometric convergence to 0 of the probability that the goal has not been encountered by the nth generation is established for a class of genetic algorithms. These algorithms employ a quickly decreasing mutation rate and a crossover which restarts the algorithm in a controlled way depending on the current population and restricts execution of this crossover to occasions when progress of the algorithm is too slow. It is shown that without the crossover studied here, which amounts to a tempered restart of the algorithm, the asserted geometric convergence need not hold.

In a repulsive point process, points act as if they are repelling one another, leading to underdispersed configurations when compared to a standard Poisson point process. Such models are useful when competition for resources exists, as in the locations of towns and trees. Bertil Matérn introduced three models for repulsive point processes, referred to as types I, II, and III. Matérn used types I and II, and regarded type III as intractable. In this paper an algorithm is developed that allows for arbitrarily accurate approximation of the likelihood for data modeled by the Matérn type-III process. This method relies on a perfect simulation method that is shown to be fast in practice, generating samples in time that grows nearly linearly in the intensity parameter of the model, while the running times for more naive methods grow exponentially.

The waste-recycling Monte Carlo (WRMC) algorithm introduced by physicists is a modification of the (multi-proposal) Metropolis–Hastings algorithm, which makes use of all the proposals in the empirical mean, whereas the standard (multi-proposal) Metropolis–Hastings algorithm uses only the accepted proposals. In this paper we extend the WRMC algorithm to a general control variate technique and exhibit the optimal choice of the control variate in terms of the asymptotic variance. We also give an example which shows that, in contradiction to the intuition of physicists, the WRMC algorithm can have an asymptotic variance larger than that of the Metropolis–Hastings algorithm. However, in the particular case of the Metropolis–Hastings algorithm called the Boltzmann algorithm, we prove that the WRMC algorithm is asymptotically better than the Metropolis–Hastings algorithm. This last property is also true for the multi-proposal Metropolis–Hastings algorithm. In this last framework we consider a linear parametric generalization of WRMC, and we propose an estimator of the explicit optimal parameter using the proposals.

In this paper we study efficient simulation algorithms for estimating P(X›x), where X is the total time of a job with ideal time T that needs to be restarted after a failure. The main tool is importance sampling, where a good importance distribution is identified via an asymptotic description of the conditional distribution of T given X›x. If T≡t is constant, the problem reduces to the efficient simulation of geometric sums, and a standard algorithm involving a Cramér-type root, γ(t), is available. However, we also discuss an algorithm that avoids finding the root. If T is random, particular attention is given to T having either a gamma-like tail or a regularly varying tail, and to failures at Poisson times. Different types of conditional limit occur, in particular exponentially tilted Gumbel distributions and Pareto distributions. The algorithms based upon importance distributions for T using these asymptotic descriptions have bounded relative error as x→∞ when combined with the ideas used for a fixed t. Nevertheless, we give examples of algorithms carefully designed to enjoy bounded relative error that may provide little or no asymptotic improvement over crude Monte Carlo simulation when the computational effort is taken into account. To resolve this problem, an alternative algorithm using two-sided Lundberg bounds is suggested.

The standard Markov chain Monte Carlo method of estimating an expected value is to generate a Markov chain which converges to the target distribution and then compute correlated sample averages. In many applications the quantity of interest θ is represented as a product of expected values, θ = µ 1 ⋯ µ k , and a natural estimator is a product of averages. To increase the confidence level, we can compute a median of independent runs. 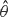The goal of this paper is to analyze such an estimator , i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for 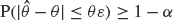to have fixed relative precision at a given level of confidence, that is, to satisfy . Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.

We study the discrete-time approximation of doubly reflected backward stochastic differential equations (BSDEs) in a multidimensional setting. As in Ma and Zhang (2005) or Bouchard and Chassagneux (2008), we introduce the discretely reflected counterpart of these equations. We then provide representation formulae which allow us to obtain new regularity results. We also propose an Euler scheme type approximation and give new convergence results for both discretely and continuously reflected BSDEs.

We consider Monte Carlo methods for the classical nonlinear filtering problem. The first method is based on a backward pathwise filtering equation and the second method is related to a backward linear stochastic partial differential equation. We study convergence of the proposed numerical algorithms. The considered methods have such advantages as a capability in principle to solve filtering problems of large dimensionality, reliable error control, and recurrency. Their efficiency is achieved due to the numerical procedures which use effective numerical schemes and variance reduction techniques. The results obtained are supported by numerical experiments.

Given a set of points in the plane, the problem of existence and finding the least absolute deviations line is considered. The most important properties are stated and proved and two efficient methods for finding the best least absolute deviations line are proposed. Compared to other known methods, our proposed methods proved to be considerably more efficient.

A weighted graph G is a pair (V, ℰ) containing vertex set V and edge set ℰ, where each edge e ∈ ℰ is associated with a weight We . A subgraph of G is a forest if it has no cycles. All forests on the graph G form a probability space, where the probability of each forest is proportional to the product of the weights of its edges. This paper aims to simulate forests exactly from the target distribution. Methods based on coupling from the past (CFTP) and rejection sampling are presented. Comparisons of these methods are given theoretically and via simulation.

While the convergence properties of many sampling selection methods can be proven, there is one particular sampling selection method introduced in Baker (1987), closely related to ‘systematic sampling’ in statistics, that has been exclusively treated on an empirical basis. The main motivation of the paper is to start to study formally its convergence properties, since in practice it is by far the fastest selection method available. We will show that convergence results for the systematic sampling selection method are related to properties of peculiar Markov chains.

We extend a result due to Zazanis (1992) on the analyticity of the expectation of suitable functionals of homogeneous Poisson processes with respect to the intensity of the process. As our main result, we provide Monte Carlo estimators for the derivatives. We apply our results to stochastic models which are of interest in stochastic geometry and insurance.

The paper deals with the asymptotic behavior of the bridge of a Gaussian process conditioned to stay in n fixed points at n fixed past instants. In particular, functional large deviation results are stated for small time. Several examples are considered: integrated or not fractional Brownian motions and m-fold integrated Brownian motion. As an application, the asymptotic behavior of the exit probability is studied and used for the practical purpose of the numerical computation, via Monte Carlo methods, of the hitting probability up to a given time of the unpinned process.

We investigate the problem of using a Riemannian sum with random subintervals to approximate the iterated Itô integral ∫wdw - or, equivalently, solving the corresponding stochastic differential equation by Euler's method with variable step sizes. In the past this task has been used as a counterexample to illustrate that variable step sizes must be used with extreme caution in stochastic numerical analysis. This article establishes a class of variable step size schemes which do work.

The problem of finding the probability distribution of the first hitting time of a double integral process (DIP) such as the integrated Wiener process (IWP) has been an important and difficult endeavor in stochastic calculus. It has applications in many fields of physics (first exit time of a particle in a noisy force field) or in biology and neuroscience (spike time distribution of an integrate-and-fire neuron with exponentially decaying synaptic current). The only results available are an approximation of the stationary mean crossing time and the distribution of the first hitting time of the IWP to a constant boundary. We generalize these results and find an analytical formula for the first hitting time of the IWP to a continuous piecewise-cubic boundary. We use this formula to approximate the law of the first hitting time of a general DIP to a smooth curved boundary, and we provide an estimation of the convergence of this method. The accuracy of the approximation is computed in the general case for the IWP and the effective calculation of the crossing probability can be carried out through a Monte Carlo method.