Refine listing
Actions for selected content:
236 results in 65Cxx
Stochastic Collocation on Unstructured Multivariate Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 03 July 2015, pp. 1-36
- Print publication:
- July 2015
-
- Article
- Export citation
American Option Valuation under Continuous-Time Markov Chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 378-401
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
On the Backward Euler Approximation of the Stochastic Allen-Cahn Equation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 323-338
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Multivariate Distributions with Fixed Marginals and Correlations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 602-608
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
On the Acceleration of the Multi-Level Monte Carlo Method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 307-322
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
The Euler Scheme for a Stochastic Differential Equation Driven by Pure Jump Semimartingales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 149-166
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Applying the Wiener-Hopf Monte Carlo Simulation Technique for Lévy Processes to Path Functionals
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 129-148
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
On the Random Sampling of Pairs, with Pedestrian Examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 292-305
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Lumpings of Markov Chains, Entropy Rate Preservation, and Higher-Order Lumpability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1114-1132
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Weak Convergence Rates of Population Versus Single-Chain Stochastic Approximation MCMC Algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1059-1083
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Exact estimation for Markov chain equilibrium expectations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 377-389
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The Containment Condition and Adapfail Algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1189-1195
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The Explicit Laplace Transform for the Wishart Process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 640-656
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Numerical Approximation of Stationary Distributions for Stochastic Partial Differential Equations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 858-873
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
Convergence of Conditional Metropolis-Hastings Samplers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 422-445
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Markov Chain Monte Carlo for Computing Rare-Event Probabilities for a Heavy-Tailed Random Walk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 359-376
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Exact Simulation for Diffusion Bridges: An Adaptive Approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 19 February 2016, pp. 346-358
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Error Bounds and Normalising Constants for Sequential Monte Carlo Samplers in High Dimensions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 279-306
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Efficient Simulation of Large Deviation Events for Sums of Random Vectors Using Saddle-Point Representations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 703-720
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
Overlap Problems on the Circle
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 773-790
- Print publication:
- September 2013
-
- Article
-
- You have access
- Export citation
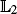 -error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is
-error of the estimate of the normalising constant associated to the target. We also establish marginal propagation of chaos properties of the algorithm. These results are deduced when the cost of the algorithm is 