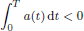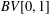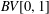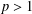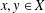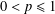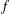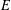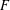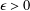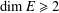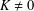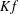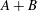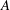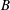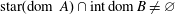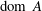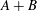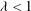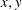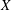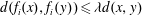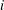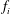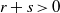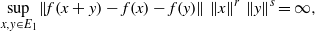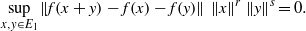Refine listing
Actions for selected content:
127 results in 47Hxx
MONOTONE OPERATORS AND THE PROXIMAL POINT ALGORITHM IN COMPLETE CAT(0) METRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 23 September 2016, pp. 70-90
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
EXISTENCE OF A WEAK SOLUTION FOR A CLASS OF FRACTIONAL LAPLACIAN EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 392-404
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
MEASURES OF NONCOMPACTNESS IN A SOBOLEV SPACE AND INTEGRO-DIFFERENTIAL EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 497-506
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
METRIC REGULARITY—A SURVEY PART II. APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 376-417
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
Pairs of positive periodic solutions of nonlinear ODEs with indefinite weight: a topological degree approach for the super–sublinear case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 449-474
- Print publication:
- June 2016
-
- Article
- Export citation
Non-trivial solutions of local and non-local Neumann boundary-value problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 07 March 2016, pp. 337-369
- Print publication:
- April 2016
-
- Article
- Export citation
Domains of accretive operators in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 07 January 2016, pp. 325-336
- Print publication:
- April 2016
-
- Article
- Export citation
ORBITALLY NONEXPANSIVE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 497-503
- Print publication:
- June 2016
-
- Article
-
- You have access
- Open access
- Export citation
FIXED POINTS THEOREMS FOR GENERALISED WEAKLY CONTRACTIVE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 321-329
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
NONLINEAR ANALYSIS IN GEODESIC METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 05 August 2015, pp. 514-515
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
UNIFORMLY BOUNDED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 463-469
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
LOCAL BOUNDEDNESS OF NONAUTONOMOUS SUPERPOSITION OPERATORS IN
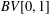 $BV[0,1]$
$BV[0,1]$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 08 July 2015, pp. 325-341
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ON HYPERSTABILITY OF ADDITIVE MAPPINGS ONTO BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 30 December 2014, pp. 278-285
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
CHEBYSHEV SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 161-231
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
On Nonlinear Boundary Conditions Involving Decomposable Linear Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 421-439
-
- Article
-
- You have access
- Export citation
SUM THEOREMS FOR MAXIMALLY MONOTONE OPERATORS OF TYPE (FPV)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 08 July 2014, pp. 1-26
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
AN EXISTENCE RESULT FOR A VARIATIONAL-LIKE INEQUALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 319-326
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
CONTRACTIVE FAMILIES ON COMPACT SPACES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 444-462
- Print publication:
- July 2014
-
- Article
- Export citation
HOLOMORPHIC SUPERPOSITION OPERATORS BETWEEN BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 186-197
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
A HYPERSTABILITY RESULT FOR THE CAUCHY EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 33-40
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
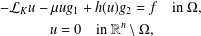
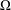
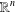
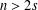
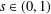
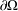
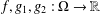
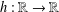
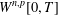
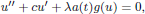
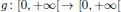 is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when
is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when