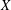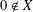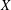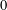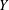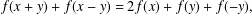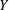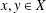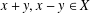Refine listing
Actions for selected content:
127 results in 47Hxx
Fixed points of multivalued maps under local Lipschitz conditions and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1467-1494
- Print publication:
- June 2020
-
- Article
- Export citation
A generalization of Krasnosel'skii compression fixed point theorem by using star convex sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 277-303
- Print publication:
- February 2020
-
- Article
- Export citation
GEOMETRIC AND FIXED POINT PROPERTIES IN PRODUCTS OF NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 262-273
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
BEST PROXIMITY POINTS AND FIXED POINTS WITH
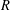 $R$-FUNCTIONS IN THE FRAMEWORK OF
$R$-FUNCTIONS IN THE FRAMEWORK OF 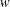 $w$-DISTANCES
$w$-DISTANCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 497-507
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
AMENABLE SEMIGROUPS OF NONLINEAR OPERATORS IN UNIFORMLY CONVEX BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 284-292
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A Strong Convergence Theorem for an Iterative Method for Finding Zeros of Maximal Monotone Maps with Applications to Convex Minimization and Variational Inequality Problems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 26 September 2018, pp. 241-257
-
- Article
- Export citation
A NEW EXTENSION OF DARBO’S FIXED POINT THEOREM USING RELATIVELY MEIR–KEELER CONDENSING OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 19 July 2018, pp. 286-297
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
MONOTONE LIPSCHITZIAN SEMIGROUPS IN BANACH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 417-428
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
NONEXPANSIVE BIJECTIONS TO THE UNIT BALL OF THE
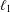 $\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES
$\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 285-292
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
A NOTE ON THE GENERALISED HYPERSTABILITY OF THE GENERAL LINEAR EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 263-273
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
SHRINKING PROJECTION ALGORITHMS FOR THE SPLIT COMMON NULL POINT PROBLEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 299-306
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
FIBONACCI–MANN ITERATION FOR MONOTONE ASYMPTOTICALLY NONEXPANSIVE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 307-316
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A Fractal Operator on Some Standard Spaces of Functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 771-786
-
- Article
- Export citation
TWO NEW GENERALISED HYPERSTABILITY RESULTS FOR THE DRYGAS FUNCTIONAL EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 269-280
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
ON THE CONVERGENCE RATE OF THE KRASNOSEL’SKIĬ–MANN ITERATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 162-170
- Print publication:
- August 2017
-
- Article
-
- You have access
- Open access
- Export citation
Coexistence Solutions for a Periodic Competition Model with Singular–Degenerate Diffusion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 1065-1075
-
- Article
- Export citation
ON APPROXIMATE SOLUTIONS OF SOME DIFFERENCE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 01 December 2016, pp. 476-481
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A PURELY METRIC PROOF OF THE CARISTI FIXED POINT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 333-337
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
On Semipositone Non-Local Boundary-Value Problems with Nonlinear or Affine Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 635-649
-
- Article
- Export citation
BEST PROXIMITY POINT THEOREMS FOR CYCLIC QUASI-CONTRACTION MAPS IN UNIFORMLY CONVEX BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 149-156
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
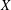
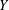
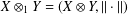
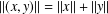
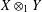
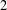
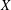
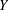
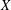
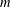
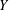
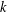
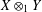
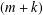
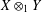
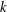
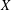
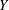
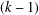
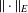
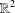
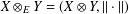
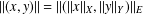
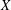
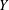
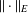
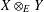
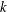
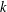
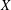
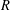
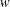

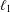
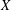
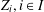

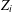
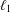
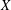
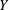
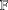
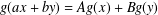
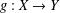
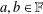
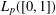
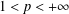
 , the space of all real-valued continuous functions defined on a compact interval
, the space of all real-valued continuous functions defined on a compact interval 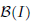 of all bounded functions and the Lebesgue space
of all bounded functions and the Lebesgue space 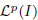 , and in some standard spaces of smooth functions such as the space
, and in some standard spaces of smooth functions such as the space 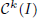 of
of 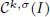 and Sobolev spaces
and Sobolev spaces 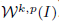 . Using properties of the
. Using properties of the