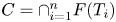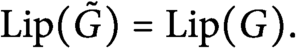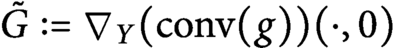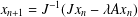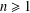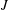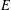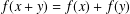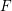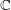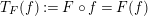Refine listing
Actions for selected content:
127 results in 47Hxx
Proof Mining with the Bounded Functional Interpretation
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 265-266
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
Bounds for a nonlinear ergodic theorem for Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1570-1593
- Print publication:
- May 2023
-
- Article
- Export citation
An asynchronous inertial algorithm for solving convex feasibility problems with strict pseudo-contractions in Hilbert spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 229-243
-
- Article
- Export citation
Existence results for a nonlinear nonautonomous transmission problem via domain perturbation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1451-1476
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic aspects of tumour–immune system interaction under a periodic immunotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 606-645
-
- Article
- Export citation
NOTES ON ORTHOGONAL-COMPLETE METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 154-160
- Print publication:
- February 2022
-
- Article
- Export citation
INVARIANT MEANS AND ACTIONS OF SEMITOPOLOGICAL SEMIGROUPS ON COMPLETELY REGULAR SPACES AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 162-173
- Print publication:
- February 2021
-
- Article
-
- You have access
- Export citation
Kirszbraun’s Theorem via an Explicit Formula
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 April 2020, pp. 142-153
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation
Steady-state solutions of one-dimensional competition models in an unstirred chemostat via the fixed point index theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 240-264
- Print publication:
- February 2021
-
- Article
- Export citation
COMPUTATION OF ZEROS OF MONOTONE TYPE MAPPINGS: ON CHIDUME’S OPEN PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 278-288
-
- Article
-
- You have access
- Export citation
On the Linearity of Order-isomorphisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 03 January 2020, pp. 399-416
- Print publication:
- April 2021
-
- Article
- Export citation
Amenability and Fixed Point Properties of Semitopological Semigroups in Modular Vector Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 692-704
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
ON APPROXIMATELY ADDITIVE MAPPINGS IN 2-BANACH SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 15 August 2019, pp. 299-310
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
ON MODULATED TOPOLOGICAL VECTOR SPACES AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 July 2019, pp. 325-332
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Asymptotic Behaviour of the Energy Integral of a Two-Parameter Homogenization Problem with Nonlinear Periodic Robin Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 985-1016
-
- Article
- Export citation
MONOTONE AND PSEUDO-MONOTONE EQUILIBRIUM PROBLEMS IN HADAMARD SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 11 March 2019, pp. 220-242
-
- Article
- Export citation
COMPOSITION OPERATORS ON WIENER AMALGAM SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 08 March 2019, pp. 257-274
-
- Article
-
- You have access
- HTML
- Export citation
APPLICATION OF PROJECTION ALGORITHMS TO DIFFERENTIAL EQUATIONS: BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 23-46
-
- Article
-
- You have access
- Export citation
Corrigendum to: Dirichlet and Neumann boundary conditions for the p-Laplace operator: What is in between?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1689-1691
- Print publication:
- December 2019
-
- Article
- Export citation