Refine listing
Actions for selected content:
221 results in 06xxx
Calculus in f-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 110-116
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
Mildly distributive semilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-315
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
On the order-theoretical foundation of a theory of quasicompactly generated spaces without separation axiom
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 2 / April 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-212
- Print publication:
- April 1984
-
- Article
-
- You have access
- Export citation
Central relations on lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 3 / December 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-372
- Print publication:
- December 1983
-
- Article
-
- You have access
- Export citation
A note on subdirectly irreducible distributive double p-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 1 / August 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 46-58
- Print publication:
- August 1983
-
- Article
-
- You have access
- Export citation
Dualities for some De Morgan algebras with operators and Lukasiewicz algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 3 / June 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-393
- Print publication:
- June 1983
-
- Article
-
- You have access
- Export citation
The distributive lattice free product as a sublattice of the abelian l-group free product
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 1 / February 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 92-100
- Print publication:
- February 1983
-
- Article
-
- You have access
- Export citation
The lattice of stable marriages and permutations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-410
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
Lattice properties of the symmetric weakly inverse semigroup on a totally ordered set
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-404
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Real order-automorphism groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-261
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
Almost distributive lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 77-91
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
The lateral completion of a completely distributive lattice-ordered group (revisited)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 114-128
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Permutation representation of groups with Boolean orthogonalities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 4 / April 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 412-418
- Print publication:
- April 1981
-
- Article
-
- You have access
- Export citation
Lattice-ordered modules of quotients
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-251
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Slim trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-214
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Prime ideal characterization of chain based lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 98-106
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
Semilattices with a transitive automorphism group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-34
- Print publication:
- February 1980
-
- Article
-
- You have access
- Export citation
The root system of primes of a Hahn group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 29 / Issue 1 / February 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-28
- Print publication:
- February 1980
-
- Article
-
- You have access
- Export citation
Uniform labelled semilattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Extensions of strict partial orders in N-Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 2 / March 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 241-249
- Print publication:
- March 1978
-
- Article
-
- You have access
- Export citation
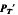 be the set of α ∈
be the set of α ∈ 