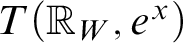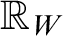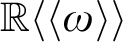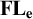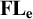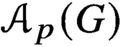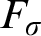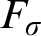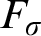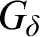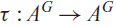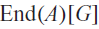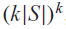Refine listing
Actions for selected content:
221 results in 06xxx
On the Axiomatisability of the Dual of Compact Ordered Spaces
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, p. 526
- Print publication:
- December 2021
-
- Article
-
- You have access
- HTML
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
MODAL OPERATORS ON RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1322-1348
- Print publication:
- December 2022
-
- Article
- Export citation
GRZEGORCZYK POINTS AND FILTERS IN BOOLEAN CONTACT ALGEBRAS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 September 2021, pp. 509-528
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SURREAL ORDERED EXPONENTIAL FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 1066-1115
- Print publication:
- September 2021
-
- Article
- Export citation
VAUGHT’S CONJECTURE FOR ALMOST CHAINABLE THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2021, pp. 991-1005
- Print publication:
- September 2021
-
- Article
- Export citation
Trees of tangles in infinite separation systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 22 July 2021, pp. 297-327
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MOST SIMPLE EXTENSIONS OF
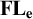 $\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
$\textbf{FL}_{\textbf{e}}$ ARE UNDECIDABLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1156-1200
- Print publication:
- September 2022
-
- Article
- Export citation
APPROXIMATING TREES AS COLOURED LINEAR ORDERS AND COMPLETE AXIOMATISATIONS OF SOME CLASSES OF TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 June 2021, pp. 1035-1065
- Print publication:
- September 2021
-
- Article
- Export citation
An approach to Quillen’s conjecture via centralisers of simple groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e48
-
- Article
-
- You have access
- Open access
- Export citation
ON WEAKLY PERFECT ANNIHILATING-IDEAL GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 11 May 2021, pp. 362-372
- Print publication:
- December 2021
-
- Article
- Export citation
TUKEY ORDER AMONG
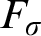 $F_{\sigma }$ IDEALS
$F_{\sigma }$ IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 06 May 2021, pp. 855-870
- Print publication:
- June 2021
-
- Article
- Export citation
CELLULAR AUTOMATA OVER ALGEBRAIC STRUCTURES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 306-319
- Print publication:
- May 2022
-
- Article
- Export citation
Bi-orders do not arise from total orders
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 217-224
- Print publication:
- March 2022
-
- Article
- Export citation
REFLEXIVITY INDEX AND IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 493-505
- Print publication:
- December 2021
-
- Article
- Export citation
COMBINATORICS OF ULTRAFILTERS ON COHEN AND RANDOM ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 109-126
- Print publication:
- March 2022
-
- Article
- Export citation
FINDING DESCENDING SEQUENCES THROUGH ILL-FOUNDED LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 817-854
- Print publication:
- June 2021
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
WEIHRAUCH GOES BROUWERIAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1614-1653
- Print publication:
- December 2020
-
- Article
- Export citation
AROUND RUBIN’S “THEORIES OF LINEAR ORDER”
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 27 October 2020, pp. 1403-1426
- Print publication:
- December 2020
-
- Article
- Export citation