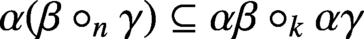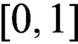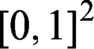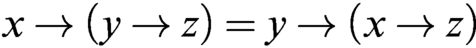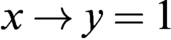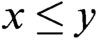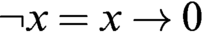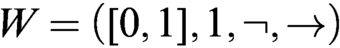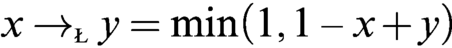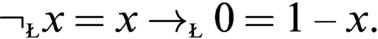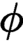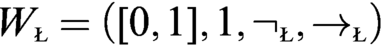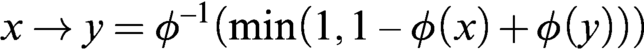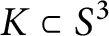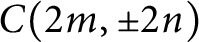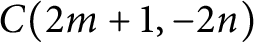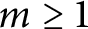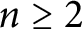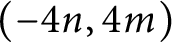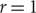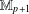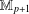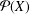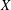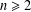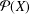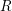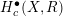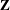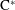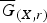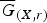Refine listing
Actions for selected content:
221 results in 06xxx
THE DISTRIBUTIVITY SPECTRUM OF BAKER’S VARIETY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 119-144
- Print publication:
- February 2021
-
- Article
- Export citation
A METRIC VERSION OF SCHLICHTING’S THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 07 September 2020, pp. 1607-1613
- Print publication:
- December 2020
-
- Article
- Export citation
WHAT THE ŁUKASIEWICZ AXIOMS MEAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 906-917
- Print publication:
- September 2020
-
- Article
- Export citation
Left orderable surgeries of double twist knots II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 27 August 2020, pp. 624-637
- Print publication:
- September 2021
-
- Article
- Export citation
Improved Ramsey-type results for comparability graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 13 August 2020, pp. 747-756
-
- Article
- Export citation
Edwards' condition for quasitraces on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 525-547
- Print publication:
- April 2021
-
- Article
-
- You have access
- Open access
- Export citation
Orders on Trees and Free Products of Left-ordered Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 335-347
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A MINIMAL CONGRUENCE LATTICE REPRESENTATION FOR
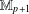 $\mathbb{M}_{p+1}$
$\mathbb{M}_{p+1}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 24 March 2020, pp. 332-340
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
RECOVERING THE BOUNDARY PATH SPACE OF A TOPOLOGICAL GRAPH USING POINTLESS TOPOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 232-248
- Print publication:
- October 2021
-
- Article
- Export citation
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Cohomology of generalized configuration spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 2 / February 2020
- Published online by Cambridge University Press:
- 20 December 2019, pp. 251-298
- Print publication:
- February 2020
-
- Article
- Export citation
Dense Orderings in the Space of Left-orderings of a Group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 17 December 2019, pp. 393-404
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Smallest weakly contractible non-contractible topological spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 11 December 2019, pp. 263-274
-
- Article
- Export citation
HEREDITARILY ANTISYMMETRIC OPERATOR ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 09 October 2019, pp. 1039-1074
- Print publication:
- May 2021
-
- Article
- Export citation
Relations and trails in lattices of projections in W*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 23 August 2019, pp. 1189-1215
-
- Article
- Export citation
On Annelidan, Distributive, and Bézout Rings
- Part of
- Modules, bimodules and ideals
- Chain conditions, growth conditions, and other forms of finiteness
- Boolean algebras (Boolean rings)
- Distributive lattices
- Local rings and generalizations
- Radicals and radical properties of rings
- Conditions on elements
- Rings and algebras arising under various constructions
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1082-1110
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Nearly Approximate Transitivity (AT) for Circulant Matrices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 07 March 2019, pp. 381-415
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A unified stability theory for classical and monotone Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 56 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 12 July 2019, pp. 1-22
- Print publication:
- March 2019
-
- Article
- Export citation
The Weak Order on Weyl Posets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 867-899
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
On Structure Groups of Set-Theoretic Solutions to the Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 683-717
-
- Article
- Export citation