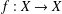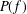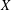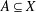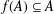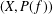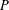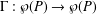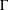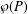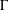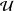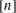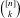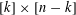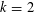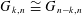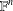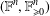Refine listing
Actions for selected content:
221 results in 06xxx
On the Weak Order of Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 299-336
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
CONTENT AND SINGLETONS BRING UNIQUE IDENTIFICATION MINORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 October 2018, pp. 67-90
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
THE LOOMIS–SIKORSKI THEOREM FOR
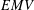 $EMV$-ALGEBRAS
$EMV$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 23 August 2018, pp. 200-234
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
Perforation conditions and almost algebraic order in Cuntz semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 18 April 2018, pp. 669-702
- Print publication:
- August 2018
-
- Article
- Export citation
An Equivariant Theory for the Bivariant Cuntz Semigroup
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 573-598
-
- Article
- Export citation
REPRESENTING REGULAR PSEUDOCOMPLEMENTED KLEENE ALGEBRAS BY TOLERANCE-BASED ROUGH SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 57-78
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
HOMOGENEOUS FUNCTIONALLY ALEXANDROFF SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 331-339
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ON THE COMPLEMENT OF THE ZERO-DIVISOR GRAPH OF A PARTIALLY ORDERED SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 185-193
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
On a random search tree: asymptotic enumeration of vertices by distance from leaves
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 850-876
- Print publication:
- September 2017
-
- Article
- Export citation
CLOSURE OPERATORS, FRAMES AND NEATEST REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 361-373
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
THE EXPECTED JAGGEDNESS OF ORDER IDEALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 March 2017, e9
-
- Article
-
- You have access
- Open access
- Export citation
ISOTONIAN ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 08 March 2017, pp. 83-101
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
NONCROSSING SETS AND A GRASSMANN ASSOCIAHEDRON
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 February 2017, e5
-
- Article
-
- You have access
- Open access
- Export citation
Von Neumann Algebras and Extensions of Inverse Semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 57-97
-
- Article
- Export citation
VARIETIES OF SKEW BOOLEAN ALGEBRAS WITH INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 September 2016, pp. 290-306
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
FINITE-DIMENSIONAL ORDERED VECTOR SPACES WITH RIESZ INTERPOLATION AND EFFROS–SHEN’S UNIMODULARITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 13 May 2016, pp. 277-287
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
- Print publication:
- April 2018
-
- Article
- Export citation
RESOLVABILITY OF MEASURABLE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 January 2016, pp. 70-79
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
CHARACTERIZATION OF PROJECTIVE QUANTALES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 403-420
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
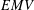
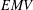
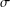
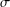
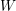
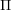
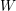

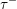
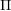
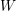
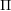
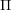
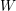
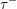
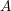
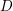
 ) in terms of Cu(
) in terms of Cu(