Marques-Smith and Sullivan [‘Partial orders on transformation semigroups’, Monatsh. Math.140 (2003), 103–118] studied various properties of two partial orders on P(X), the semigroup (under composition) consisting of all partial transformations of an arbitrary set X. One partial order was the ‘containment order’: namely, if α,β∈P(X) then α⊆β means xα=xβ for all x∈dom α, the domain of α. The other order was the so-called ‘natural order’ defined by Mitsch [‘A natural partial order for semigroups’, Proc. Amer. Math. Soc.97(3) (1986), 384–388] for any semigroup. In this paper, we consider these and other orders defined on the symmetric inverse semigroup I(X) and the partial Baer–Levi semigroup PS(q). We show that there are surprising differences between the orders on these semigroups, concerned with their compatibility with respect to composition and the existence of maximal and minimal elements.

We prove that there are permutation classes (hereditary properties of permutations) of every growth rate (Stanley–Wilf limit) at least λ≈2.48187, the unique real root of x5−2x4−2x2−2x−1, thereby establishing a conjecture of Albert and Linton.

The main purpose of this paper is to develop a point-free notion of topological transitivity. First, we define transitive frame maps and transitive completely prime filters in Frm, the category of frames and frame maps. Then we discuss the relationship between these notions in Frm and the notions of topological transitive and transitive points in Top. Finally, we investigate the relationship between transitive frame maps and the existence of transitive completely prime filters.

In this paper we consider a class of quasi-birth-and-death processes for which explicit solutions can be obtained for the rate matrix R and the associated matrix G . The probabilistic interpretations of these matrices allow us to describe their elements in terms of paths on the two-dimensional lattice. Then determining explicit expressions for the matrices becomes equivalent to solving a lattice path counting problem, the solution of which is derived using path decomposition, Bernoulli excursions, and hypergeometric functions. A few applications are provided, including classical models for which we obtain some new results.

We prove that every for every complete lattice-ordered effect algebra E there exists an orthomodular lattice O(E) and a surjective full morphism øE: O(E) → E which preserves blocks in both directions: the (pre)imageofa block is always a block. Moreover, there is a 0, 1-lattice embedding : E → O(E).

We introduce perfect effect algebras and we show that every perfect algebra is an interval in the lexicographical product of the group of all integers with an Abelian directed interpolation po-group. To show this we introduce prime ideals of effect algebras with the Riesz decomposition property (RDP). We show that the category of perfect effect algebras is categorically equivalent to the category of Abelian directed interpolation po-groups. Moreover, we prove that any perfect effect algebra is a subdirect product of antilattice effect algebras with the RDP.

We show that monotone σ -complete effect algebras under some conditions are σ - homomorphic images of effect-tribes (as monotone σ -complete effect algebras), which are nonempty systems of fuzzy sets closed under complements, sums of fuzzy sets less than 1, and containing all pointwise limits of nondecreasing fuzzy sets. Because effect-tribes are generalizations of Boolean σ -algebras of subsets, we present a generlization of the Loomis-Sikorski theorem for such effect algebras. We show that we can choose an effect-tribe to be a system of affin fuzzy sets. In addition, we present a new version of the Loomis-Sikorski theorem for σ-complete MV-algebras.

The conjugacy classes of so-called special involutions parameterize the constituents of the action of a finite Coxeter group on the cohomology of the complement of its complexified hyperplane arrangement. In this note we give a short intrinsic characterisation of special involutions in terms of so-called bulky parabolic subgroups.

In this note we characterize the abelian groups G which have two different proper subgroups N and M such that the subgroup lattice L(G)=[0, M]∪ [N, G] is the union of these intervals.

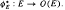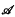The optimality of dualities on a quasivariety , generated by a finite algebra 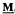, has been introduced by Davey and Priestley in the 1990s. Since every optimal duality is determined by a transversal of a certain family of subsets of Ω, where Ω is a given set of relations yielding a duality on 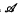, an understanding of the structures of these subsets—known as globally minimal failsets—was required. A complete description of globally minimal failsets which do not contain partial endomorphisms has recently been given by the author and H. A. Priestley. Here we are concerned with globally minimal failsets containing endomorphisms. We aim to explain what seems to be a pattern in the way endomorphisms belong to these failsets. This paper also gives a complete description of globally minimal failsets whose minimal elements are automorphisms, when 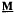is a subdirectly irreducible lattice-structured algebra.

Pseudoeffect (PE-) algebras generalize effect algebras by no longer being necessarily commutative. They are in certain cases representable as the unit interval of a unital po-group, for instance if they fulfil a certain Riesz property.

Several infinitary lattice properties and the countable Riesz interpolation property are studied for PE-algebras on the one hand and for po-groups on the other hand. We establish the exact relationships between the various conditions that are taken into account, and in particular, we examine how properties of a PE-algebra are related to the analogous properties of a representing po-group.

Let A be a uniformly complete vector sublattice of an Archimedean semiprime f-algebra B and p ∈ {1, 2,…}. It is shown that the set ΠBp (A) = {f1 … fp: fk ∈ A, k = 1, …, p } is a uniformly complete vector sublattice of B. Moreover, if A is provided with an almost f-algebra multiplication * then there exists a positive operator Tp, from ΠBp(A) into A such that fi *…* fp = Tp(f1 …fp) for all f1…fp ∈ A.

As application, being given a uniformly complete almost f-algebra (A, *) and a natural number p ≧ 3, the set Π*p(A) = {f1 *… *fp: fk ∈ A, k = 1…p} is a uniformly complete semiprime f-algebra under the ordering and the multiplication inherited from A.

Generalizing earlier results of Katriňák, El-Assar and the present author we prove new structure theorems for l-algebras. We obtain necessary and sufficient conditions for the decomposition of an arbitrary bounded lattice into a direct product of (finitely) subdirectly irreducible lattices.

Generalizing and strengthening some well-known results of Higman, B. Neumann, Hanna Neumann and Dark on embeddings into two-generator groups, we introduce a construction of subnormal verbal embedding of an arbitrary (soluble, fully ordered or torsion free) ordered countable group into a twogenerator ordered group with these properties. Further, we establish subnormal verbal embedding of defect two of an arbitrary (soluble, fully ordered or torsion free) ordered group G into a group with these properties and of the same cardinality as G, and show in connection with a problem of Heineken that the defect of such an embedding cannot be made smaller, that is, such verbal embeddings of ordered groups cannot in general be normal.

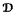Consider the quasi-variety generated by a finite algebra 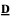and assume that 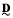yields a natural duality on based on which is optimal modulo endomorphisms. We shoe that, provided satisfies certain minimality conditions, we can transfer this duality to a natural duality on based on , which is also optimal modulo endormorphisms, for any finite algebra 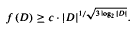in that has a subalgebra isomorphic to .

Pseudo-BL algebras are noncommutative generalizations of BL-algebras and they include pseudo-MV algebras, a class of structures that are categorically equivalent to l-groups with strong unit. In this paper we characterize directly indecomposable pseudo-BL algebras and we define and study different classes of these structures: local, good, perfect, peculiar, and (strongly) bipartite pseudo-BL algebras.

We give a characterization of nuclear Fréchet lattices in terms of lattice properties of the seminorms. Indeed, we prove that a Fréchet lattice is nuclear if and only if it is both an AL- and an AM-space.

In this paper, the variety of three-valued closure algebras, that is, closure algebras with the property that the open elements from a three-valued Heyting algebra, is investigated. Particularly, the structure of the finitely generated free objects in this variety is determined.

A subset F of an ordered set X is a fibre of X if F intersects every maximal antichain of X. We find a lower bound on the function ƒ (D), the minimum fibre size in the distributive lattice D, in terms of the size of D. In particular, we prove that there is a constant c such that In the process we show that minimum fibre size is a monotone property for a certain class of distributive lattices. This fact depends upon being able to split every maximal antichain of this class of distributive lattices into two parts so that the lattice is the union of the upset of one part and the downset of the other.

Let K and L be lattices, and let ϕ be a homomorphism of K into L.Then ϕ induces a natural 0-preserving join-homomorphism of Con K into Con L.

Extending a result of Huhn, the authors proved that if D and E are finite distributive lattices and ψ is a 0-preserving join-homomorphism from D into E, then D and E can be represented as the congruence lattices of the finite lattices K and L, respectively, such that ψ is the natural 0-preserving join-homomorphism induced by a suitable homomorphism ϕ: K → L. Let m and n denote the number of join-irreducible elements of D and E, respectively, and let k = max (m, n). The lattice L constructed was of size O(22(n+m)) and of breadth n+m.

We prove that K and L can be constructed as ‘small’ lattices of size O(k5) and of breadth three.