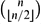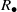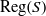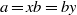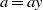Refine listing
Actions for selected content:
221 results in 06xxx
Local Maxima of Quadratic Boolean Functions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 21 December 2015, pp. 633-640
-
- Article
- Export citation
ON COLIMITS OVER ARBITRARY POSETS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 22 July 2015, pp. 219-228
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
THE NATURAL PARTIAL ORDER ON LINEAR SEMIGROUPS WITH NULLITY AND CO-RANK BOUNDED BELOW
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 104-115
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
THE REFLEXIVITY INDEX OF A LATTICE OF SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 237-250
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
GLOBAL DETERMINISM OF CLIFFORD SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 16 May 2014, pp. 63-77
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
THE ZELEZNIKOW PROBLEM ON A CLASS OF ADDITIVELY IDEMPOTENT SEMIRINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 05 September 2013, pp. 404-420
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
A DUALIZING OBJECT APPROACH TO NONCOMMUTATIVE STONE DUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 19 August 2013, pp. 383-403
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
REGULAR CONGRUENCES ON AN IDEMPOTENT-REGULAR-SURJECTIVE SEMIGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 30 July 2013, pp. 190-196
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
THE NATURAL PARTIAL ORDER ON SOME TRANSFORMATION SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 279-292
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
NON-POINTED EXACTNESS, RADICALS, CLOSURE OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 348-361
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
IRREDUCIBLE QUASIORDERS OF MONOUNARY ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 01 March 2013, pp. 259-276
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
VARIETIES WHOSE TOLERANCES ARE HOMOMORPHIC IMAGES OF THEIR CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 August 2012, pp. 326-338
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
A NOTE ON RELATIVE PSEUDOCOMPACTNESS IN THE CATEGORY OF FRAMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 May 2012, pp. 120-130
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
THE GELFAND SPECTRUM OF A NONCOMMUTATIVE C*-ALGEBRA: A TOPOS-THEORETIC APPROACH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 39-52
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
SIMPLE EXTENSIONS OF COMBINATORIAL STRUCTURES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 193-214
- Print publication:
- July 2011
-
- Article
- Export citation
REAL IDEALS IN POINTFREE RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 338-352
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
ON THE PARTITION MONOID AND SOME RELATED SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 06 December 2010, pp. 273-288
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
ON THE LOOMIS–SIKORSKI THEOREM FOR MV-ALGEBRAS WITH INTERNAL STATE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 01 April 2011, pp. 317-333
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
TYPE DECOMPOSITION OF A PSEUDOEFFECT ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 28 February 2011, pp. 335-358
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
A NONCOMMUTATIVE GENERALIZATION OF STONE DUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 05 May 2010, pp. 385-404
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation