Refine listing
Actions for selected content:
221 results in 06xxx
Covering in the lattice of subuniverses of a finite distributive lattice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-353
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
Posets and differential graded algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-19
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Varieties of distributive lattices with unary operations I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-207
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
Maximal sublattices and Frattini sublattices of bounded lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 110-127
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Certain extensions and factorizations of α-complete homomorphisms in archimedean lattice-ordered groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 239-258
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
The Nachibin quasi-uniformity of a bi-Stonian space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 3 / December 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-326
- Print publication:
- December 1996
-
- Article
-
- You have access
- Export citation
The higher Stasheff-Tamari posets
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-154
- Print publication:
- June 1996
-
- Article
- Export citation
Random high-dimensional orders
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 161-184
- Print publication:
- March 1995
-
- Article
- Export citation
The vector lattice cover of certain partially ordered groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 352-367
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
Lattice-ordered power series fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 3 / June 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-321
- Print publication:
- June 1992
-
- Article
-
- You have access
- Export citation
Vector lattices over subfields of the reals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 359-375
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
The associated order of a preorder
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-24
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Epicompletetion of archimedean l–groups and vector lattices with weak unit
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 25-56
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
Pasting infinite lattices
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-21
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Boolean near-rings and weak commutativity
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-107
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
A note on uniform ordered spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-352
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
Lattices of homomorphisms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 3 / June 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-406
- Print publication:
- June 1986
-
- Article
-
- You have access
- Export citation
Biordered sets are biordered subsets of idempotents of semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-268
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Extension and inversion of extended orthomorphisms on Riesz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-242
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Positive derivations on partially ordered strongly regular rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 178-180
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
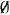 ) corresponding to the empty poset is always contained in
) corresponding to the empty poset is always contained in 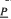 ) of distributive lattices with unary operations, extending work of Cornish. The generating algebra (
) of distributive lattices with unary operations, extending work of Cornish. The generating algebra (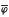 with
with 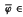 Hom
Hom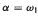 and
and 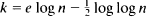 is a threshold function for the appearance of an element of degree
is a threshold function for the appearance of an element of degree 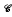 (
( ∈ Orth
∈ Orth