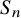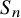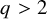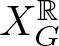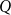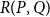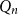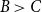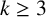Refine listing
Actions for selected content:
221 results in 06xxx
Hypercontractivity on the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 January 2024, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ordered Groups, Computability and Cantor-Bendixson Rank
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 29 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 23 February 2024, p. 664
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
BETWEENNESS ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 November 2023, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomology of a real toric variety and shellability of posets arising from a graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 03 November 2023, pp. 1044-1084
-
- Article
- Export citation
AN ALGEBRAIC PROOF OF COMPLETENESS FOR MONADIC FUZZY PREDICATE LOGIC
 $\mathbf {MMTL}\boldsymbol {\forall }$
$\mathbf {MMTL}\boldsymbol {\forall }$
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 18 October 2023, pp. 213-239
- Print publication:
- March 2025
-
- Article
- Export citation
ALGEBRAIC SEMANTICS FOR RELATIVE TRUTH, AWARENESS, AND POSSIBILITY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 154-177
- Print publication:
- March 2024
-
- Article
- Export citation
WEAK WELL ORDERS AND FRAÏSSÉ’S CONJECTURE
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 September 2023, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘ON THE COMPLEMENT OF THE ZERO-DIVISOR GRAPH OF A PARTIALLY ORDERED SET’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 170-173
- Print publication:
- February 2024
-
- Article
- Export citation
A NOTE ON BRØNDSTED’S FIXED POINT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 161-166
- Print publication:
- August 2024
-
- Article
- Export citation
Corrigendum: Von Neumann algebras and extensions of inverse semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 919-922
-
- Article
-
- You have access
- HTML
- Export citation
A NATURAL DEDUCTION SYSTEM FOR ORTHOMODULAR LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 910-949
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Semidistrim Lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 16 June 2023, e50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REFLEXIVITY INDEX OF THE PRODUCT OF SOME TOPOLOGICAL SPACES AND LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 376-387
- Print publication:
- April 2024
-
- Article
- Export citation
CANONICITY IN POWER AND MODAL LOGICS OF FINITE ACHRONAL WIDTH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 March 2023, pp. 705-735
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boolean algebras, Morita invariance and the algebraic K-theory of Lawvere theories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 253-270
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTUITIONISTIC SAHLQVIST THEORY FOR DEDUCTIVE SYSTEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 February 2023, pp. 1522-1580
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Poset Ramsey numbers: large Boolean lattice versus a fixed poset
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 17 February 2023, pp. 638-653
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WHEN IS A NUMERICAL SEMIGROUP A QUOTIENT?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 67-76
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Morse theory of Bestvina–Brady type for posets and matchings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 209-220
- Print publication:
- February 2024
-
- Article
- Export citation
Residual torsion-free nilpotence, bi-orderability, and two-bridge links
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 25 January 2023, pp. 394-457
- Print publication:
- April 2024
-
- Article
- Export citation