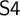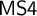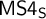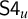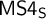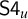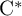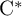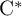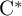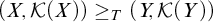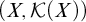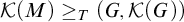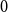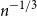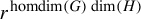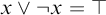Refine listing
Actions for selected content:
221 results in 06xxx
LOCAL FINITENESS IN VARIETIES OF MS4-ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Order-automorphism groups of Archimedean ordered groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 628-633
- Print publication:
- June 2025
-
- Article
- Export citation
Vines and MAT-labeled graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 20 December 2024, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RANKS OF SOFT OPERATORS IN NOWHERE SCATTERED
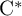 $\mathrm {C}^*$-ALGEBRAS
$\mathrm {C}^*$-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 371-410
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ORDER-PRESERVING EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 17 December 2024, pp. 91-107
- Print publication:
- February 2025
-
- Article
- Export citation
A ONE-PAGE PROOF OF A THEOREM OF BELEZNAY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, pp. 536-537
- Print publication:
- December 2024
-
- Article
- Export citation
Regular Schur labeled skew shape posets and their 0-Hecke modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 27 November 2024, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equality cases of the Alexandrov–Fenchel inequality are not in the polynomial hierarchy
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
- Export citation
STRICTLY n-FINITE VARIETIES OF HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From real-life to very strong axioms. Classification problems in Descriptive Set Theory and regularity properties in Generalized Descriptive Set Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 November 2024, pp. 285-286
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
The Galvin property under the ultrapower axiom
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 27 May 2024, pp. 1686-1717
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Noise sensitivity of the minimum spanning tree of the complete graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 23 May 2024, pp. 708-723
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complexity of non-abelian cut-and-project sets of polytopal type I: special homogeneous Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 13 May 2024, pp. 175-217
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Structural, point-free, non-Hausdorff topological realization of Borel groupoid actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 March 2024, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IDEMPOTENT GENERATORS OF INCIDENCE ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 488-497
- Print publication:
- December 2024
-
- Article
- Export citation
DUALITY FOR COALGEBRAS FOR VIETORIS AND MONADICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1022-1055
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COFINAL TYPES OF ULTRAFILTERS OVER MEASURABLE CARDINALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 February 2024, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the cross-product conjecture for the number of linear extensions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 535-562
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEGREE OF SATISFIABILITY IN HEYTING ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2024, pp. 533-551
- Print publication:
- June 2025
-
- Article
- Export citation