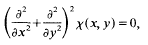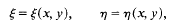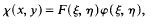Refine listing
Actions for selected content:
416 results in 35Jxx
Generalized Emden-Fowler equations of subcritical growth
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 254-262
-
- Article
-
- You have access
- Export citation
A posteriori error estimates for elliptic boundary-value problems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-168
-
- Article
-
- You have access
- Export citation
Second-order strongly elliptic operators on Lie groups with Hölder continuous coefficients
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-363
-
- Article
-
- You have access
- Export citation
Multiplicity theorems for semilinear elliptic problems depending on a parameter
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 171-180
-
- Article
-
- You have access
- Export citation
Multiplicity of positive solutions for a class of problems with critical growth in ℝN
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 1-21
-
- Article
-
- You have access
- Export citation
Infinitely many arbitrarily small solutions for singular elliptic problems with critical Sobolev–Hardy exponents
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 97-108
-
- Article
-
- You have access
- Export citation
ON SCHRÖDINGER EQUATIONS WITH INDEFINITE NONLINEARITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 115-128
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
MINIMAL GRAPHS WITH DISCONTINUOUS BOUNDARY VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 75-95
-
- Article
-
- You have access
- Export citation
EXISTENCE OF POSITIVE EVANESCENT SOLUTIONS TO SOME QUASILINEAR ELLIPTIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 1 / August 2008
- Published online by Cambridge University Press:
- 01 August 2008, pp. 157-162
- Print publication:
- August 2008
-
- Article
-
- You have access
- Export citation
ON A CLASS OF SOBOLEV FUNCTIONS AND ITS APPLICATIONS TO HIGHER-ORDER ELLIPTIC EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 405-417
-
- Article
-
- You have access
- Export citation
MULTIPLE SOLUTIONS FOR A DIRICHLET PROBLEM WITH p-LAPLACIAN AND SET-VALUED NONLINEARITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 285-303
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
SYMMETRY RESULT FOR SOME OVERDETERMINED VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 479-494
-
- Article
-
- You have access
- Export citation
Positive solutions for Dirichlet problems of singular quasilinear elliptic equations via variational methods
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 187-202
- Print publication:
- December 2004
-
- Article
- Export citation
Scattering of tidal waves by reefs and spits
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 355-370
- Print publication:
- December 2000
-
- Article
- Export citation
Multiple solutions for semilinear elliptic problems
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 307-317
- Print publication:
- December 2000
-
- Article
- Export citation
On transformations of the biharmonic equation
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-130
- Print publication:
- June 1985
-
- Article
- Export citation
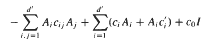 in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients
in divergence form corresponding to a quadratic form with complex coefficients, bounded Hölder continuous principal coefficients 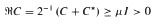 uniformly over
uniformly over 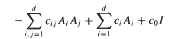 in non-divergence form for which the principal coefficients are at least once differentiable.
in non-divergence form for which the principal coefficients are at least once differentiable.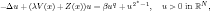
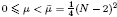 . We obtain the existence of infinitely many solutions for the singular critical problem
. We obtain the existence of infinitely many solutions for the singular critical problem 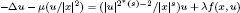 with Dirichlet boundary condition for suitable positive number λ.
with Dirichlet boundary condition for suitable positive number λ.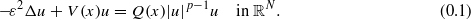
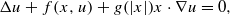
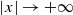 under quite general assumptions upon
under quite general assumptions upon 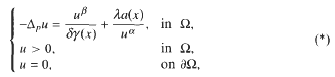
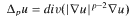 , 1 <
, 1 <